Арифметические прогрессии, компьютерные сети и случайная неслучайность. За что математики Григорий Маргулис и Гиллель Фюрстенберг получили премию Абеля
Теоретическая математика высоко ценится, однако ее достижения не так часто оказывают непосредственное влияние на прикладные науки, — и тем ценнее случаи, когда они оказываются напрямую связаны с практической деятельностью. Именно так обстоят дела с идеями одного из героев этого материала. «Нож» рассказывает об исследованиях Григория Маргулиса и Гиллеля Фюрстенберга, благодаря которым они стали лауреатами Абелевской премии 2020 года.
Вчера, 18 марта 2020 года, была вновь вручена Премия Абеля — одна из двух важнейших математических наград. В отличие от медали Филдса, которая вручается раз в 4 года четырем ученым, не достигшим еще 40 лет и занятым в разных областях науки, премия Абеля вручается ежегодно 1 или 2 работающим в одной и той же области заслуженным исследователям.
В этом году лауреатами премии стали российско-американский математик Григорий Маргулис (Йельский университет, ИППИ РАН) и американо-израильский ученый Гиллель Фюрстенберг (Ивритский университет в Иерусалиме), ставшие, согласно официальной формулировке, «пионерами в области применения теории вероятностей и динамики к теории чисел, теории групп и комбинаторике».
Если говорить простым языком, то основные достижения Маргулиса и Фюрстенберга связаны со вскрытием роли случайности в неслучайном: с тем, как свойства случайных перемещений и случайных «смен взгляда» на пространство могут давать нам представление о его устройстве.
Представим себя туристом, гуляющим по незнакомому городу и выбирающим на каждом повороте, куда ему свернуть, при помощи подбрасывания монетки. Что мы сможем узнать из этого блуждания о городской планировке? Это ближайший бытовой образ, который может дать нам представление о работах лауреатов.
Одним из самых ярких достижений Гиллеля Фюрстенберга стал новый, вероятностный, метод доказательства теоремы Семереди об арифметических прогрессиях. Последняя утверждает следующее: рассмотрим подмножество A целых чисел положительной плотности — то есть такое, что найдется бесконечная последовательность чисел N1, N2.., Ni.., для которой доля чисел из A на отрезке от -Ni до Ni будет больше некоторого фиксированного положительного числа или, говоря грубее, чисел из A не бесконечно мало по отношению ко всем целым числам. Тогда в A можно найти сколь угодно длинные последовательности чисел, отстоящих друг от друга на одно и то же расстояние (арифметические прогрессии).
Это утверждение было сформулировано в качестве гипотезы Полем Эрдёшем и Палом Тураном в 1936 году, в 1975 году его впервые доказал Андре Семереди (лауреат Абелевской премии 2012 года). Доказательство Семереди базировалось на теории графов, а через 2 года Гиллель Фюрстенберг смог связать недавно доказанную теорему с теорией динамических систем.
Он понял, что гипотеза Эрдёша — Турана связана с преобразованиями множества целых чисел, сохраняющих свойства, связанные с разными способами «измерения объема» подмножеств, при этом случай, доказанный Семереди, соответствует преобразованию, которое прибавляет единицу к каждому целому числу.
Один из компонентов доказательства Фюрстенберга можно связать с вышеупомянутой идеей случайного блуждания: набора перемещений по пространству, в котором мы каждый раз забываем, куда шли до этого, и выбираем новое направление подбрасыванием монетки. Оказывается, если мы ходим по прямой или плоскости, то в случайном блуждании мы почти всегда вернемся в начальную точку, если же пространство трехмерно — то в начальной точке мы когда-либо вновь окажемся лишь примерно в трети случаев.
Идеи Фюрстенберга впоследствии легли в основу доказательства теоремы Грина-Тао (2004 г.) о том, что множество простых чисел содержит арифметические прогрессии сколь угодно большой длины.
К центральным идеям и результатам Григория Маргулиса найти доступную иллюстрацию гораздо сложнее, однако наблюдение, сделанное им для коллег-прикладников в самом начале творческого пути (1973 г.), стало основой для создания важной области компьютерных наук: теории графов-экспандеров (расширителей).
Возьмем компьютерную сеть: мы хотели бы, чтобы в ней было как можно меньше связей между компьютерами — тогда сеть будет дешевле; но сеть должна быть максимально надежной, и чтобы при этом можно было бы разорвать много связей без ущерба для сети. Теория экспандеров отвечает на вопрос о том, как этого добиться.
Граф — это набор точек, соединенных ребрами. В полном графе между каждой парой точек есть ребро. В разреженных графах ребра очень редки. Графы-экспандеры можно весьма приблизительно определить как разреженные графы, в которых тем не менее из каждой точки можно дойти в любую другую по ребрам множеством способов (высокая связность). Маргулис нашел первый пример бесконечной последовательности графов с всё возрастающим числом вершин, в которых, с одной стороны, количество ребер, исходящих из каждой точки по мере роста числа вершин, не менялось, а с другой — количество способов перемещения между разными вершинами никогда не падало ниже определенного числа.
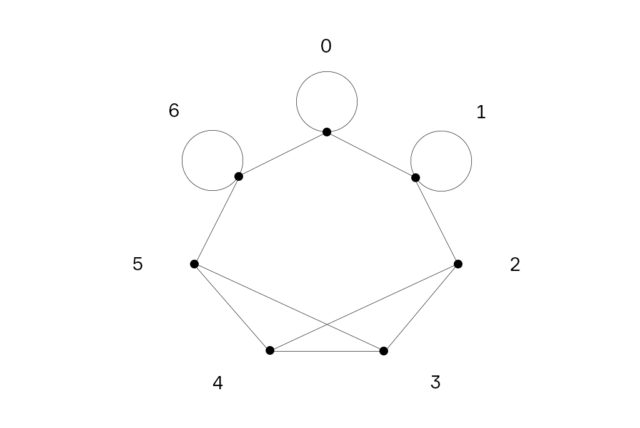
Чем дальше находится граф в этой последовательности — тем более он разрежен, но, несмотря на это, он всё так же связен. Существование подобных последовательностей ранее доказал Марк Пинскер, но его доказательство было неконструктивным: из него нельзя было получить ни одного конкретного примера.
В своем доказательстве Маргулис использовал методы, связанные с теорией представлений и свойством Каждана (Т). Те же методы использовались в его наиболее глубоких исследованиях в теории дискретных подгрупп групп Ли, теории чисел и римановых многообразий. История открытия экспандеров — один из тех редких случаев, когда чистая математика неожиданно нашла свой путь в прикладную. Сегодня наука об экспандерах широко применяется в теории сложности алгоритмов, теории кодирования и даже в нейронауках.