Альтруизм и окраска шкур. Как математика помогает биологам — и наоборот

Что такое математическая биология и зачем она нужна

Все способы математического описания биологических процессов укладываются в общую дисциплину под названием «математическая биология». Абсолютно всё, что только можно представить в биологии — от передачи импульса в клетках до эволюционных процессов, — можно описать какими-либо математическими формулами.

В нашей древней истории науки по сути представляли собой одну большую «супернауку» — никто, например, не отделял физику от биологии. Наука о живом, как и большинство других областей знания, изначально была скорее описательной. Понятия эксперимента и уж тем более математического подхода появились относительно человеческой и научной истории недавно — когда, как и в древности, научное знание стало проникать из одной области в другую, снова объединяя до того разделенные сферы. Не в последнюю очередь математика проникла в биологию из-за появления в последней смежных с другими науками поддисциплин — биоинформатики, биофизики, биохимии. Тут-то и появилось новое понимание математики как некоего универсального языка, способного описать практически всё что угодно.

Условно можно разделить математические подходы в биологии на две большие группы. Во-первых, математика описывает уже существующие процессы: например, скорость роста стебля, взаимоотношение видов в экосистеме и т. д. Всё живое на Земле подчиняется единым законам бытия: оно растет, размножается, подчиняясь в той или иной степени генетическому коду, живет и умирает. Вполне логично, что жизнь всех существ в мире можно описать определенными формулами.

Во-вторых, при помощи математических методов можно моделировать ситуации. Моделирование в последние годы стало важным подходом в биологии и биоинформатике — именно так ученые не только тестируют те или иные предположения, но и предсказывают, например, возможные конформации белка или имитируют поведение мышцы при введении в нее ионов или каких-то веществ. Моделирование иногда даже помогает ученым лучше понять предполагаемые взаимодействия между молекулами на клеточном уровне, то есть заглянуть туда, куда заглянуть просто так довольно сложно. Через биологию моделирование проникло и в медицину — теперь ученые-медики могут создавать модели распространения вируса и исследовать развитие рака. Именно моделирование последнее время привлекает к себе огромное внимание.

Фракталы и структурная гармония природы

Фракталами называют самоподобные структуры. Если вы когда-нибудь видели кочан капусты романеско (это близкий родственник цветной капусты), то вы знаете, что такое фрактал: конусы романеско состоят из конусов поменьше, а те из конусов еще меньше и так далее, и так далее… Изначально фракталами занималась только математика, причем до конца XIX века довольно эпизодически. Потом потихоньку математики приступили к изучению алгебраических фракталов, и уже после пришло время фракталов природных.

В природе фрактальная структура встречается повсеместно. Иногда она видна невооруженным взглядом или по крайней мере достаточно крупная, чтобы ее заметить. К примерам таких фракталов можно отнести как всё ту же романеско, так и, например, наши легкие. Если вы когда-нибудь обращали внимание на их строение, то могли заметить, что они ветвятся: трахея разделяется на два бронха, те делятся на трубки поменьше и так далее, и так далее, пока всё в итоге не оканчивается альвеолами.

Некоторые считают фракталом и кровеносную систему, и корневые системы трав и деревьев.

Иногда же фракталы запрятаны глубоко во внутренней или молекулярной структуре организма. Последнее, кстати, встречается довольно часто: ряд ученых считает самым ярким примером молекулярного фрактала ДНК, нуклеиновую кислоту, которая занимается хранением и передачей генетической информации абсолютно у всех организмов, населяющих планету, за исключением некоторых вирусов.

Еще одной интересной математической идеей, описывающей природные структуры, является понятие золотого сечения — идеальной пропорции, структурной гармонии. Золотое сечение — это ситуация, при которой отношения частей целого между собой и наибольшей части к общему целому равны. Принципам структурной гармонии в той или иной степени подчиняется строение всего — и живого, и неживого: от расположения листьев на ветке (это позволяет каждому получать больше солнечного света) до галактик. Вы наверняка видели немало картинок, на которые была наложена золотая спираль Фибоначчи. При этом многие ученые уточняют: раковина аммонита выглядит так не потому, что она фрактал, а потому, что фрактал лучшего всего описывает именно эту организацию.

Теория игр и треугольник взаимоотношений

Изначально теорию игр разработали для экономики — одну из главных ролей в ее создании сыграл математик Джон Нэш, по мотивам жизни которого сняли оскароносный фильм «Игры разума». Впоследствии оказалось, что под эту теорию попадает множество других, не социальных, а природных явлений — например, взаимоотношение видов, а точнее их поведения, внутри единой экосистемы.

Согласно эволюционной теории игр, выживаемость особи зависит не столько от ее качеств, сколько от стратегии, которую она выбирает при встрече с представителем другого вида — убегать или драться, подчиняться или подчинять. В зависимости от выбранной стратегии особь может проиграть или выиграть. При встрече с представителем своего вида особь может быть агрессивной — но проиграть перед лицом хищника, а может проявить дружелюбие для формирования кооперации — и потенциально защититься, но потерять часть ресурсов и сил, поскольку теперь будет тратить их не только на себя.

Эволюционная теория игр оказалась поразительно полезной. С ее помощью удалось объяснить несколько до того не понятных стратегий — например, альтруизм, который, казалось бы, не имеет никакого смысла в рамках принятой теории эволюции.

Однако стратегии с более низким шансом на успех постепенно исчезают из популяции, и остаются только те, что обеспечивают больший шанс на выживание, — они ведут себя почти как живые существа, где выживает наиболее приспособленный. У особи, выбравшей стратегию альтруизма — помощь соседу в ущерб собственной выживаемости, — потенциально появляется шанс, что когда-нибудь так же поступит сосед, и это как раз таки повысит общую приспособляемость.

Кроме того, некоторые модели помогли лучше понять взаимоотношение видов внутри сообществ, и сюда входят не только порой очень запутанные пищевые цепочки, но и взаимопомощь.

Моделирование работы систем организма и шкур животных

На практикумах по физиологии человека и животных студенты прошлых лет при исследовании функционирования сердца прибегали к экспериментам на животных. Теперь это во многих случаях не нужно — существуют хорошие модельные системы, и, «добавляя» какую-либо молекулу, можно «получить» воздействие на это выдуманное сердце. Какие еще системы можно моделировать и что ученые благодаря этому получают?

На самом деле математических моделей, применяемых в биологических исследованиях, множество. Существуют модели кровеносной системы — так изучают, например, влияние отдельных органов на давление, распространение лекарственных препаратов по крови и даже их воздействие на организм в целом. Есть модели работы иммунной системы, и последнее время ученые активно исследуют возможности таких «симуляторов» — с их помощью можно, например, предположить, как именно и с каким комплексом будет связываться патоген, что особенно важно в условиях возможных пандемий.

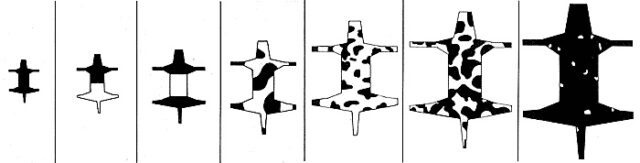
Но моделировать можно не только актуальные для медицины и физиологии процессы — те же принципы применимы, например, к моделированию окраски шкур животных. Такую модель предложил математик Джеймс Д. Мюррей (эта статья есть и на русском языке) в попытках ответить на вопрос, почему же у млекопитающих возможно такое множество самых разных окрасок. Он предположил, что все варианты окраски определяются единым механизмом, который включается на этапе эмбриогенеза. Математическая модель Мюррея работала так хорошо, что на выходе получались результаты, удивительно сопоставимые с реальными окрасами шкур самых разных зверей — от зебры до гепарда.

Пятна и полосы на шкурах появляются из-за работы специальных клеток — меланоцитов. Меланоциты выделяют пигмент меланин, который и окрашивает шерсть. Причем меланинов бывает два: эумеланин, дающий черно-коричневую окраску, и феомеланин, делающий шерсть рыжей. Первым заинтересовался вопросом возникновения окраски Алан Тьюринг (тот самый, именем которого назван тест Тьюринга). Он предположил, что окраска шкуры зависит от определенных предструктур, образованных неравномерной концентрацией пигмента. И Тьюринг, и в дальнейшем Мюррей использовали в своих работах понятие реакционно-диффузионной модели — модели, описывающей химическую реакцию с одновременной диффузией веществ. Считается, что одно из веществ в этой модели может быть активатором меланоцитов, под воздействием которого они производят меланин, а другое — ингибитором, полностью блокирующим выработку меланина.

Пространственно при активной выработке и того и другого будут образовываться кластеры меланина среди пространства «не-выработки» — то есть пятна. Также Мюррей предположил, что на окраску влияет размер животного: чем оно крупнее, тем больше будут пятна, а на наиболее крупном звере пятна сольются, образовав почти полностью однотонную шкуру.

При этом у мелких зверей, скорее всего, пятен не будет вовсе, просто отдельные части шкуры будут полностью окрашены в один цвет.

Нейронные сети

Лучший пример идеи, которая проникла из биологии в математику и информатику, — это нейронные сети, разговоры о которых последнее время не будоражат разве что только тех, кто живет в полном отрыве от интернета. Дело в том, что нервные клетки, или нейроны, перманентно находятся в одном из двух состояний — возбуждения либо покоя. Это удивительно похоже на то, как создаются компьютеры и подобные им системы. Старые компьютеры строились по той же схеме просто потому, что сама идея «включено : выключено», «0 : 1» очевидна. Идея же создания огромных «думающих» систем, повторяющих работу нейронной сети, хоть и появилась давно, реализовываться стала относительно недавно, причем в последние годы человечество подобралось к ее воплощению максимально близко.

Сначала немного теории. Нейрон — клетка нервной ткани — представляет собой клетку с отростками. Один из них очень длинный и называется аксоном, остальные более мелкие и называются дендритами. Аксон оканчивается небольшим расширением, синаптическим бугорком, и формирует синапс — место контакта между двумя нейронами или, например, нейроном и мышцей. Дендриты нейрону нужны именно для соединения с другими нейронами, а синапсы служат своего рода хабами информации. Именно в синапс из нейрона выделяются нейромедиаторы. Откуда нейрон «знает», когда именно их выделять? Здесь на помощь приходит… электричество. Оно, конечно, не такое, как в проводах, но тоже представляет собой электрическое движение — нервный импульс.

Получая от соседнего нейрона сигнал — импульс, — нейрон «понимает», что нужно выделить нейромедиаторы, активируя иннервируемую ткань, либо передать импульс дальше, пустив его к другому нейрону. Нервные импульсы распространяются при помощи ионов — так образуется потенциал действия, нервное возбуждение, распространяющееся по мембране клетки. В норме в спокойном состоянии ионы с разных сторон мембраны формируют сильную разницу потенциалов — это стартовая точка, потенциал покоя (0), когда внутри потенциал сильно меньше, чем снаружи. Такая разница достигается за счет того, что внутри клетки очень много калия и отрицательно заряженных биологических молекул, а снаружи много ионов натрия. Но вот пришел сигнал от соседнего нейрона, его нужно передать дальше, и на поверхности мембраны открываются натрий-калиевые насосы, запускающие внутрь клетки натрий, — это провоцирует быстрое смещение заряженности, появление потенциала действия (1).

Получается, что нейрон может находиться в двух состояниях — 0, когда импульс не проводится, и 1, когда импульс передается дальше. Между собой нейроны связаны миллионами связей — на то и нужны десятки дендритов у каждой клетки.

Всё это стало прототипом современных компьютерных нейронных сетей. Пока что создание реального аналога человеческого (или хотя бы животного) мозга представляется невозможным, но и имеющиеся сети обучаются так быстро, что это поражает воображение.

Заключение

У многих из нас со школы сложные отношения с математикой — она кажется большинству сухой, неинтересной и скучной. На деле же математика — это всего лишь способ описания мира, ключ, при помощи которого можно открыть те двери, которые пока что закрыты, — и с каждым годом открытых дверей становится всё больше. Другое дело, что за ними оказываются десятки других, всё еще запертых, но это уже совершенно другая история.