Течения, звуки и квантовые системы. За что Александр Логунов и Евгения Малинникова получили премию Клэя?
В 2017 году два математика российского происхождения — работающий в Санкт-Петербурге и Тель-Авиве Александр Логунов и профессор Норвежского института науки и технологий Евгения Малинникова — получили премию Клэя. Впервые этой престижной награды были удостоены ученые, родившиеся и защитившие диссертации в России. Ранее лауреатами становились автор доказательства Великой теоремы Ферма Эндрю Уайлз, создатель некоммутативной геометрии Алан Конн, Эдвард Виттен, известный своей теорией струн, Теренс Тао и Бен Грин, доказавшие наличие сколь угодно длинных арифметических прогрессий во множестве простых чисел, и др.
Карлос Кёниг рассказывает о результатах Александра Логунова и Евгении Малинниковой на конференции, посвященной вручению премии Клэя.
В чем же состоят открытия Логунова и Малинниковой? В чем их важность для других областей знания? Конечно, в рамках популярной статьи дать полный ответ на этот вопрос не получится, но можно проиллюстрировать некоторые их идеи и основные выводы, прибегнув к физическим аналогиям.
Представим, что мы плаваем с аквалангом в толще огромного, уходящего в бесконечность океана. Течения уносят нас в ту или другую сторону. Для каждой точки водного пространства задана скорость течения — ее величина и направленность. Если в океане нет вихрей и воронок, то оказывается достаточным задать скорость для каждой точки лишь одним числом — потенциалом скорости — вместо набора чисел (вектора). Сама же скорость течения будет определяться тем, как потенциал меняется вблизи той области, где мы оказались. Иными словами, она становится градиентом потенциала скорости. Неформально потенциал скорости можно понимать как импульс давления, который нужно придать воде так, чтобы она текла заданным образом.
Понятие потенциала скорости впервые ввел французский ученый Жозеф Луи Лагранж в своей книге «Аналитическая механика», изданной в 1788 году.
Функция потенциала скорости обладает замечательным свойством — она является гармонической. С точки зрения физики это соответствует предположению о несжимаемости воды: сколько текущей жидкости входит в любую область, столько же из нее и вытекает.
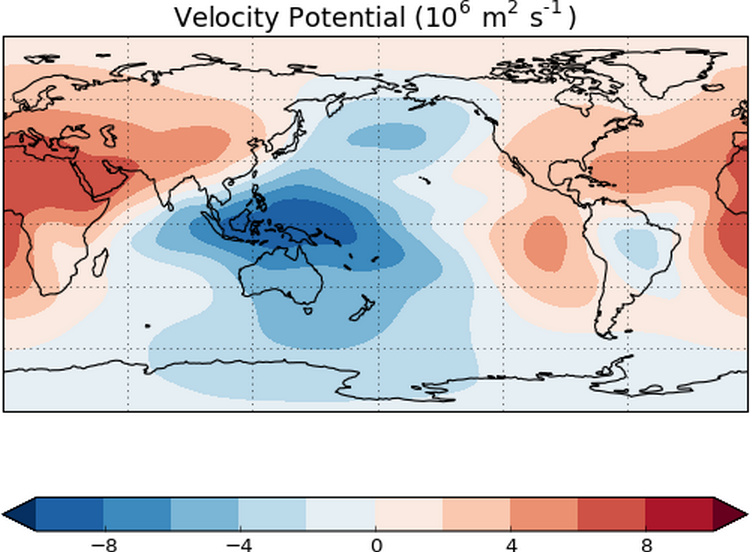
Среди математических свойств гармонической функции прежде всего стоит назвать принцип максимума: если потенциал непостоянен (то есть наблюдаются течения), то его максимум или минимум в любой области океана всегда находится на ее границе. Другие свойства описаны в теореме Лиувилля: если океан заполняет все пространство и вода движется, то существуют точки, где потенциал принимает любое возможное значение, — и в теореме о среднем: потенциал скорости в центре любой выделенной нами сферы является средним от потенциалов скоростей на его границе. В 2016 году Александр Логунов добавил к этим свойствам еще одно: площадь поверхности, составленной из точек с фиксированным значением потенциала, бесконечна. В частности, это означает, что такие поверхности не являются ограниченными — не могут быть размещены внутри шара какого-либо диаметра.
Гармонические функции встречаются отнюдь не только в гидро- и аэродинамике — науках о движении жидкости и газа. Ключевую роль они играют и в электростатике — разделе физики, изучающем не изменяющиеся во времени электрические поля, а также в небесной механике, исследующей законы движения небесных тел.
Утверждение Логунова о поверхностях с одинаковым потенциалом является лишь одним из следствий основных результатов, к которым пришли он и Малинникова. Для лучшего понимания их концепции перейдем от трехмерной гидродинамической картинки к иллюстрации, казалось бы, более простой, двухмерной.
Зададимся вслед за Хендриком Лоренцем, Германом Вейлем, Липманом Берсом и Марком Кацем следующим вопросом: «Как услышать форму барабана?»
Можно ли определить очертания барабанной мембраны по звукам, ею издаваемым? Этой проблеме и обсуждению известных фактов была посвящена статья Марка Каца. Она вышла в 1966 году в ведущем американском журнале American Mathematical Monthly, популяризирующем «царицу наук». За свою работу автор в 1968 году был удостоен престижной премии Шовене, присуждаемой за популярное изложение математических идей.
При ударе по инструменту в ряде случаев мембрана будет равномерно колебаться в нескольких постоянных частотах — чистых тонах. Наша задача состоит в том, чтобы получить максимум информации о барабане, зная лишь набор его возможных чистых тонов.
Математически описанная ситуация есть не что иное, как задача о собственных значениях оператора Лапласа (или лапласиана). Он задается в декартовых координатах суммой вторых производных функции. Геометрически его можно понимать как величину, на которую деформация мембраны в какой-то из точек отличается от средней деформации на границе ее небольшой окрестности. При игре на барабане в чистом тоне результат применения оператора Лапласа к деформации будет прямо пропорционален самой деформации, коэффициентом же пропорциональности окажется квадрат частоты. Возникающая в этом случае деформация является собственной функцией оператора, а квадрат частоты — собственным значением.
Вопрос о форме барабана тем самым обретает математическую постановку. Мы задаем две области на плоскости. Рассмотрим всевозможные функции в этих областях, постепенно становящиеся нулевыми вблизи границы барабана: она не колеблется, поскольку жестко закреплена. Могут ли две разные области иметь одинаковый спектр (набор собственных значений, множество чистых тонов) лапласиана? Это одна из так называемых обратных спектральных задач.
Первым шагом на пути к ее решению стал закон Германа Вейля, доказанный им в 1911 году. Теорема была ответом на поставленный голландским физиком Хендриком Лоренцем в 1910 году вопрос, связанный с теорией излучения, которую развивал американский математик, физик и астроном Джеймс Джинс. Вейль доказал, что, зная набор чистых тонов, мы имеем возможность определить площадь мембраны. Уточненную формулировку этого тезиса, в которой такой набор связывается не только с площадью барабана, но и с его периметром, предложил советский математик Виктор Иврий лишь в 1980 году.
Лекция Виктора Иврия о законе Вейля
Ответ на вопрос о том, можем ли мы определить геометрическую форму барабана по его чистым тонам, оказался не таким однозначным. В 1992 году Кэролин Гордон, Дэвид Уэбб и Скотт Вольперт опубликовали в Бюллетене Американского математического общества статью «Форму барабана нельзя услышать». Они построили два одинаково звучащих инструмента разной конфигурации (но одной и той же площади и периметра). Мембраны эти имели совершенно непривычный внешний вид — они представляли собой невыпуклые многоугольники.
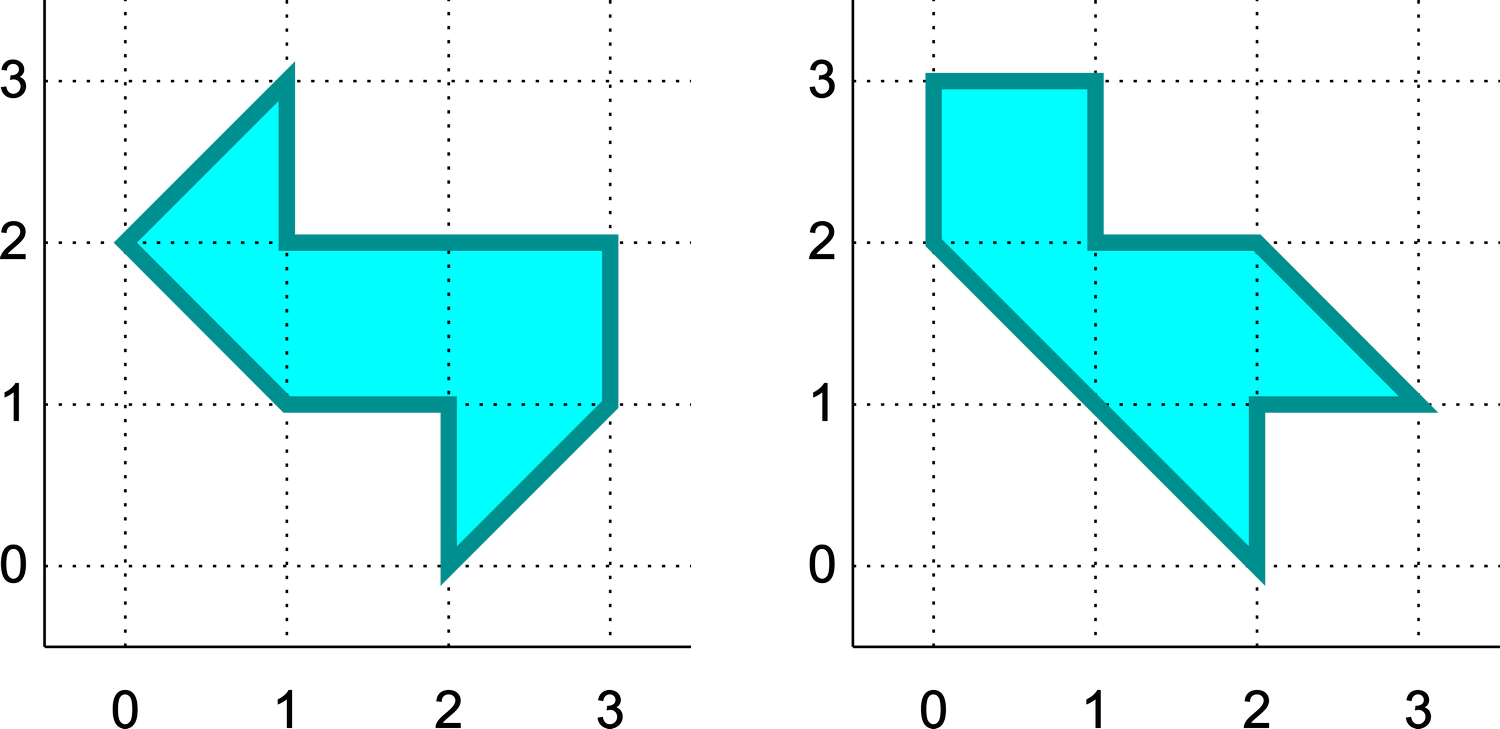
В полном доказательстве, опубликованном в том же году в журнале Inventiones mathematicae, использованы методы японца Тошикадзу Сунады. Они основаны на идеях теории чисел и связаны с изучением действий конечных групп на римановых многообразиях. За популярное изложение результатов этого исследования в журнале American Scientist Гордон и Уэбб получили премию Шовене в 2001 году.
Однако, как выяснилось в 1999-м, барабаны обычные — чья мембрана симметрична, а стенки не имеют изломов — различить по звуку все-таки можно. Доказательство этого утверждения приводится в статье Стива Зелдича из американского Северо-Западного университета.
Спектральным задачам для оператора Лапласа и его обобщений посвящены и работы Логунова и Малинниковой, но если прежде в задаче о форме барабана ученых волновало в первую очередь множество собственных чисел лапласиана, то здесь центром рассмотрения становится множество собственных функций, а точнее геометрия поверхностей, образуемых их нулями. Этими вопросами занимается особая область науки, называемая нодальной геометрией.
Для того чтобы попытаться понять ее смысл и значение, нам придется перейти к третьему физическому сюжету. Из гидродинамики и математической теории музыки мы перемещаемся в квантовую механику.
Хорошо известно, что чем точнее указываются координаты квантовой частицы, тем менее определенной становится ее скорость. Это так называемое соотношение неопределенностей Гейзенберга. Да и само положение у такой частицы появляется только в момент ее наблюдения, а до этого имеет смысл говорить лишь о вероятности ее нахождения в той или иной области пространства.
Изменение состояния частицы или же квантовой системы во времени описывается уравнением Шредингера для волновой функции. Квадрат модуля последней определяет плотность вероятности обнаружения системы в заданной точке (иными словами, вероятность ее обнаружения в малой окрестности). Множество точек, где волновая функция равна нулю, то есть где квантовую систему не обнаружить, называется ее нодальным множеством.
В 2013 году Анета Стодольна, Марк Враккинг и ряд других ученых смогли при помощи квантового микроскопа впервые напрямую увидеть нодальные множества атома водорода в электрическом поле.
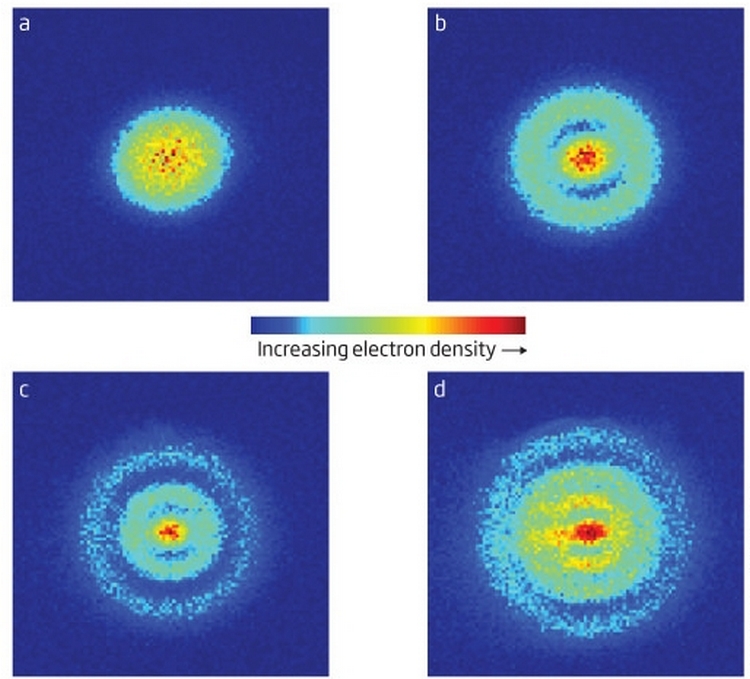
В 1982 году американский математик китайского происхождения Шин-Тун Яу сформулировал следующую гипотезу: на ограниченной и замкнутой поверхности площадь нодального множества квантовой частицы приблизительно пропорциональна квадратному корню из ее энергии, и чем эта энергия больше — тем точнее и приближение.
Через 6 лет Харольд Доннелли и Чарльз Фефферман доказали гипотезу Яу для так называемых вещественно-аналитических поверхностей. Это широкий класс объектов, но одним из их характеристических свойств является жесткость. Всю такую поверхность можно восстановить по маленькому ее кусочку.
Однако гипотеза оставалась недоказанной для гладких поверхностей: с одной стороны они не имеют изломов, а с другой их можно как угодно деформировать в том или ином месте, не изменяя в другом. Именно этим случаем и занялись герои нашей статьи.
Александр Логунов полностью доказал нижнюю оценку в гипотезе Яу. Для этого ему потребовалось доказать другое утверждение — гипотезу ныне работающего в основном в Марселе московского математика Николая Надирашвили о гармонических функциях, предложенную им в 1997 году. Она сводится к следующему. Возьмем гладкую поверхность. Рассмотрим на ней шар единичного радиуса. Тогда площадь лежащих в шаре нулей любой гармонической функции, равной нулю в его центре, можно оценить снизу положительным числом, зависящим только от поверхности и шара, но не от самой функции. Непосредственным следствием гипотезы Надирашвили оказывается и новое свойство гармонических функций, о котором было сказано выше.
Верхние оценки Логунова и Малинниковой 2016 года не закрывают вопрос с гипотезой Яу, однако существенно приближают ученых к ее доказательству. Карлос Кёниг в своем докладе на состоявшейся в конце сентября конференции, посвященной вручению премии Клэя, сообщил, что полное доказательство верхних оценок было получено уже в 2017 году лауреатами совместно с Николаем Надирашвили и Федором Назаровым. Но эти результаты, по-видимому, еще не опубликованы — и, быть может, окончательно не проверены…
В коротком популярном тексте можно лишь попытаться проиллюстрировать неформальные мотивации и упрощенные версии некоторых утверждений. Настоящее же их понимание, а тем более понимание соответствующих доказательств, требует серьезнейшей математической подготовки в специальных разделах анализа и дифференциальной геометрии.