Пьяные прогулки в неизвестность. Что такое случайные процессы и как они связаны с дрейфом генов, поездками на такси и очередями в супермаркетах
Случайные процессы описывают фондовые рынки и эволюцию популяций, принятие решений и передвижение бактерий — и очень много других явлений. Математик и художник Давид Кац — о том, сколько раз нужно тасовать колоду карт, почему пьяница в трехмерном пространстве потеряется, а на прямой далеко не уйдет, и как цепи Маркова помогают проснуться по будильнику.
О реальности вероятности
Прежде всего, когда мы говорим о любой вероятности, надо держать в фокусе одно соображение — в рамках большинства описываемых далее процессов вероятности не существует.
Этот тезис означает, что когда мы, например, подбрасываем монетку, мы просто прикладываем к физическому телу определенную силу. Таким образом, у монетки существует вполне конкретное уравнение движения, мы можем рассчитать положение монетки в любой последующий момент времени, а при необходимости — посчитать количество оборотов.
Коротко эту мысль сформулировал Эйнштейн: Бог не играет в кости.
Тем не менее на примере с монеткой отлично видно и то, почему мы вероятностные модели применяем в том числе в таких ситуациях.
Дело в том, что объем вычислений, связанных с движением даже одной монетки, довольно велик при любых разумных ограничениях на точность.
Не слишком велик для компьютера, но определенно слишком велик для человеческого мозга. Если монеток становится две или более, количество проблем у нас стремительно растет. В то же время для более-менее приличной монетки и при любом вменяемом поведении бросающего монетку модель, вообще не учитывающая усилие бросающего и определяющая вероятность орла как 0.5 и решки как 0.5, дает на удивление адекватные результаты на больших числах.
Нетрудно заметить, что в предыдущем предложении есть сразу три допущения, которые в рамках науки, вообще говоря, неплохо бы точно определить: качественная монетка, адекватное поведение бросающего, большое количество испытаний. Мы в данной статье этого делать не будем и не без интереса предлагаем читателям поупражняться в аккуратном определении этих понятий.
Случайные процессы
Прежде чем говорить о случайных процессах, поговорим о неслучайных. Что такое процесс? Ответ на этот вопрос зависит от контекста, но достаточно часто мы подразумеваем под процессом функцию. Например, процесс передвижения автомобиля — функция, которая прошедшему времени сопоставляет пройденное автомобилем расстояние. Если, например, за руль сел аккуратный водитель, которому некуда спешить, то машина едет с постоянной скоростью без ускорения, а расстояние будет со временем линейно расти. Если же водитель станет постоянно ускоряться, графиком будет уже кривая линия, «задирающаяся» вверх. Чем больше будет ускорение, тем сильнее будет задираться линия графика.
Теперь давайте представим, что мы вызвали такси и заранее не знаем, какой водитель нам попадется — некоторые из них будут гнать, другие будут ускоряться и замедляться по ведомым только им причинам, третьи не будут никуда спешить.
Таким образом, у нас есть различные функции протекания нашего процесса, которые выбираются случайным образом, и даже многократно проезжая один и тот же маршрут на такси, мы вряд ли дважды попадем на одного и того же водителя.
Как оказывается, такой очень общий подход позволяет исследовать огромное количество процессов — в химии и биологии, физике и экологии, компьютерных науках, криптографии и обработке сигналов.
Одномерный случай случайного блуждания
Разговор об одном из простейших типов случайных процессов — случайном блуждании — мы начнем с одномерного случайного блуждания с целочисленными координатами.
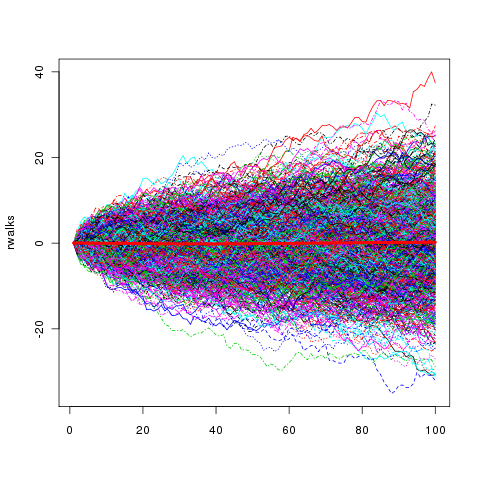
Представьте, что вы стоите на точке 0 числовой прямой. Вы можете перемещаться только по соседним целым числам и двигаетесь вправо или влево с одинаковой вероятностью, равной 0.5. Если вы проведете несколько экспериментов с листом бумаги и монеткой, то сможете пронаблюдать достаточно причудливые перемещения «взад-вперед», во многом благодаря которым задачу о том, с какой вероятностью вы доберетесь до некоторой точки, иногда называют задачей о пьянице.
Как выясняется, вероятность того, что пьяница, двигающийся каждый шаг в случайном направлении, уйдет от своей стартовой точки, весьма невысока.
Вот, например, сразу целый набор симуляций данного процесса — по горизонтали количество ходов, по вертикали — координата пьяницы.
Интересный разворот этой задачи дает фактически просто иная ее формулировка. Давайте представим, что вы играете со своим знакомым — подбрасываете монетку. Если выпадает орел, вы отдаете другу рубль, если выпадает решка — он отдает рубль вам. Возникает вопрос: с какой вероятностью вы или ваш друг проиграетесь в ноль при заданных начальных средствах, а также сколько в среднем будет протекать игра?
Несмотря на кажущуюся простоту, решение задачи потребовало применения довольно серьезного математического аппарата.
Читайте также
Еще одно довольно интересное приложение этой казалось бы несложной задачи — принятие решений. Есть подробная (но англоязычная) статья об этом, например, тут.
Неплохой способ оценки вероятности дает следующее построение. Давайте посмотрим, где и каким количеством способов мы можем оказаться за n шагов.
На нулевом ходу у нас есть единственная возможность оказаться в точке 0 и ничего более.
На первом ходу мы можем оказаться в двух точках, 1 и −1, в каждой ровно одним способом.
На втором ходу мы можем либо вернуться в ноль (двумя способами — из 1 и из −1), либо шагнуть дальше и оказаться в точках 2 или −2 (ровно одним способом в каждом случае).
Нетрудно продолжить эту последовательность, но давайте изобразим ее в виде таблицы.
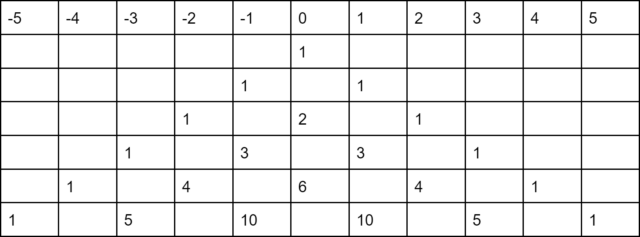
Как можно заметить, это (о чудо!) не что иное, как известный многим треугольник Паскаля.
Двумерная и более версии случайного блуждания
Еще более интересными картинки становятся, когда мы выходим на двумерную решетку (для простоты целочисленную).
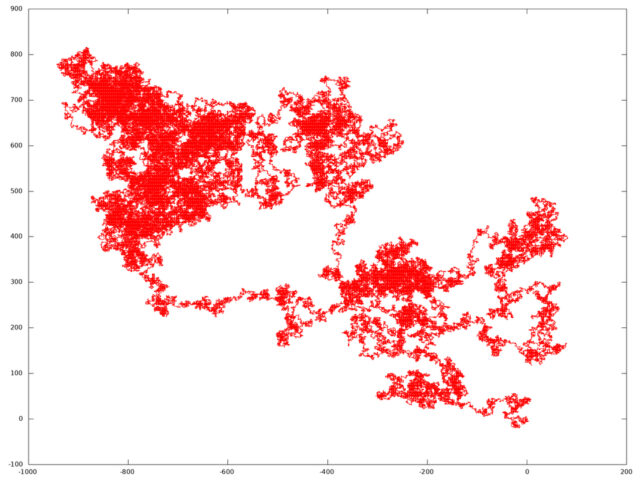
Вот один из найденных примеров траектории точки при случайном двумерном блуждании со стартом в точке (0, 0) после миллиона шагов.
Интересно, что если мы поставим задачу о том, сможет ли пьяница, гуляющий по городу, вернуться в точку, с которой он начал свой маршрут, то в двумерном случае это весьма вероятно, а вот с повышением размерности эта вероятность быстро снижается.
В случае повышения размерностей также обнаруживаются и фрактальные свойства получаемых структур — конечно, не в прямом смысле (поскольку наша фигура состоит из отдельных точек, она дискретна), — но при увеличении масштаба мы будем наблюдать самоподобие.
Случайное блуждание нередко используют для описания броуновского движения (конечно, с определенной точностью).
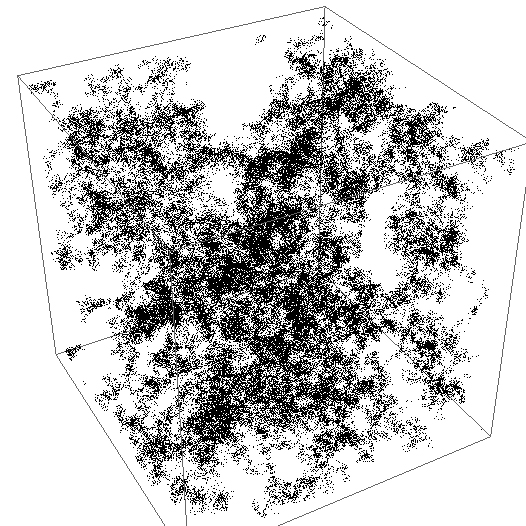
Структуры, получаемые в качестве траектории трехмерного блуждания, используются для моделирования пористых сред — картинка выше неплохо иллюстрирует почему. Другое физическое применение — моделирование процессов диффузии.
Генетикам известно и другое применение случайного блуждания — так называемый дрейф генов, случайное изменение частот аллелей, происходящее в небольшой популяции при смене поколений. Такие эффекты возникают, например, в ситуации бутылочного горлышка.
В целом приложения различных версий случайного блуждания почти безграничны — их применяют для описания возбуждения нейронов в головном мозге, в психологии в рамках исследования вероятности принятия решений со временем, для описания цепочки построения полимеров, при изучении движения бактерий и во множестве других областей.
Другой любопытный результат, полученный с помощью аппарата случайного блуждания, утверждает, что достаточно семи перетасовок, чтобы полностью перемешать колоду карт.
Модификации случайного блуждания
Наиболее распространенные модификации случайного блуждания с любым количеством измерений включают прежде всего неклассические решетки. Проще всего здесь разрешить на двумерном клетчатом поле двигаться по диагонали, но, конечно, интереснее задать клетки иным способом — например, рассмотреть решетку из треугольников или шестиугольников на плоскости. Отдельный класс решеток состоит и вовсе не из решеток в прямом смысле — мы можем блуждать по некоторому графу, вершинам, соединенным некоторым набором ребер.
Другой распространенный способ модификации — альтернативное распределение вероятности. В одномерном случае замена 0.5 и 0.5 на 0.6 и 0.4 создаст некоторую тенденцию к движению влево, но для большего количества измерений и свобода для модификаций выше. В случае графа с определенными на каждом ребре вероятностями перехода мы получаем интересный инструмент для анализа и принятия решений.
Марковские цепи
Другой простой крайне полезный тип случайных процессов — так называемые Марковские цепи. Марковской цепью называется последовательность случайных событий (количество исходов на практике часто конечно, но в определении — хотя бы счетно), таких, что вероятность наступления некоторого события в последовательности зависит только от текущего события, а не от всей предыдущей цепочки событий — то есть будущее не зависит от прошлого, только от настоящего.
Например, допустим, что вы поставили будильник на каждый час, начиная с 8:00. В 8:00 будильник звонит, и с вероятностью в 0.7 вы можете проснуться, а с вероятностью 0.3 выключите этот будильник и продолжите спать до 9:00. Если вы продолжили спать, то независимо от того, сколько раз вы уже выключали будильник, вы снова проснетесь с вероятностью 0.7 или продолжите спать с вероятностью 0.3. Конечно, вероятности перейти из второго состояния в первое или остаться в нем не обязаны совпадать с предыдущим случаем: например, вероятность уснуть из пробужденного состояния по итогам часа может быть 0.1, а вероятность продолжить активность — 0.9.
Марковские цепи активно применяются в так называемой теории массового обслуживания, или теории очередей. Количество посетителей, которые придут в магазин в тот или иной момент времени, является случайной величиной, при этом ресурсы торговых сетей ограничены, но наша задача состоит в том, чтобы эффективно воспользоваться этими ресурсами. Возможно, глубина проблемы «очередь» не вполне понятна наиболее молодым из читателей (несмотря на то, что этой проблеме посвящены даже настольные игры), но схожие проблемы возникают в ситуации передачи информации через ограниченный канал — например, в работе телекоммуникаций.
В целом Марковские цепи дают инструментарий для любых случаев, когда у нас есть некоторый входной поток событий, который мы не можем контролировать или просчитать заранее. Это могут быть приходящие посетители, выручка предприятия, а могут быть и движущиеся частицы.
Другое распространение цепей Маркова — всевозможные прогнозы, от погодных данных до ценовых трендов.
Заключение
Случайными процессами описывается удивительно широкий класс явлений: от природных эффектов до социальных процессов, от систем обслуживания до карточных игр и ценовых трендов. Так часто бывает в математике — совершенно разные объекты описываются одинаковым или очень похожим образом. Это неудивительно, если воспринимать математику как науку о связях — в этом смысле не так важно, какую точно систему мы рассматриваем, если связи в ней выстраиваются похожим образом. Это создает большой потенциал — иногда мы замечаем, что какое-то явление похоже на что-то знакомое нам, и это позволяет использовать известный нам аппарат. В данном случае в качестве такой связки выступает вероятностный подход, и несмотря на допущения, о которых мы говорили в начале статьи, он не теряет в точности, а вместо этого открывает большой новый мир, недоступный более прямолинейными методами.