Странные геометрические явления в жизни и в искусстве

Наша история начинается в 1936 году, когда небольшая семья евреев-литваков Мандельброт переезжает из Варшавы в Париж, где молодой Бенуа Мандельброт попадает под влияние своего дяди, Шолема Мандельбройта, математика и члена знаменитой группы математиков, публиковавшейся под псевдонимом Бурбаки. С самого начала юноша демонстрирует нестандартные подходы даже к решенным задачам. Вынужденный скрываться во время войны под страхом смерти, он продолжает заниматься математикой с помощью одного из участников Сопротивления, раввина Давида Фейерверкера.

После войны, завершив образование и получив докторскую степень, Мандельброт начал работать в научно-исследовательском центре IBM. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики.

В экономике его привлекли графики цен с их случайными в течение короткого периода колебаниями. Именно на них он заметил закономерности, которые до него не замечал никто. И они стали зачатком современного представления о фрактале. Сам Бенуа Мандельброт иногда называл то, чем он занимался, «искусством неровности» и работой с «неконтролируемым элементом в жизни».

Мы не будем здесь подробно рассказывать о фракталах и их месте в окружающем мире — этому посвящены сотни статей, книг и фильмов, как достаточно старых, так и новых. Однако на всякий случай напомним концепт буквально на одном примере, а затем подчеркнем несколько фактов, которые понадобятся нам в дальнейшем.

Фрактал в узком (и немного расплывчатом) смысле этого слова — фигура, обладающая свойством самоподобия. Это означает, что фигура полностью или приближенно совпадает по форме с частью самой себя. В качестве примера можно провести кривую Коха:

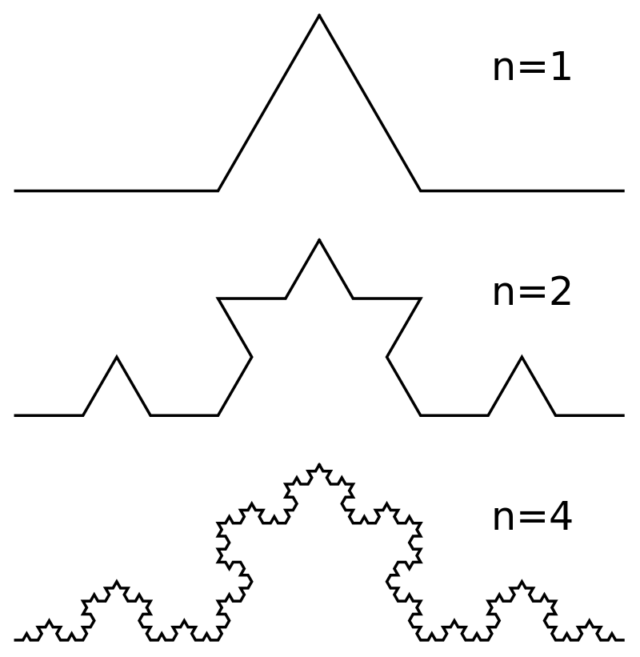
В качестве нулевого «поколения» берем просто отрезок. На первом шаге его среднюю треть превращаем в правильный треугольник без основания, как бы выгибаем его. У нас получится четыре соединенных в кривую линию отрезка. На следующем шаге повторяем эту операцию с каждым из четырех отрезков. И так далее до бесконечности. Полученная в итоге кривая и будет называться кривой Коха. Это был пример, а теперь перейдем к фактам.

Для исследования геометрических свойств фракталов используют фрактальные размерности (или метрические характеристики) — их довольно много, но наиболее известна, наверное, размерность Минковского (она же размерность Колмогорова, или box counting dimension). Она определяется следующим образом. Фигуру, размерность которой нам нужно посчитать, мы покрываем минимально возможным количеством множеств диаметра (для простоты можно считать, что кругов), затем берем отношение логарифмов с одинаковым основанием от количества таких множеств, которое нам понадобилось, и самого (перед этим логарифмом лучше поставить «-» по причинам, которые будут понятны из следующего предложения). Затем мы берем предел от этого отношения по , стремящемуся к 0 (конечно, нижний логарифм при этом станет отрицательным, поэтому нам нужен минус, чтобы это скомпенсировать). То есть мы делаем диаметр наших множеств очень-очень маленьким и смотрим, как ведет себя это отношение. Коротко всё это можно записать в виде формулы:

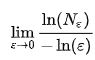
Читателю предлагается проверить самостоятельно, что такая размерность прямой линии или отрезка равна 1, а квадрата — 2, что хорошо соответствует нашим представлениям о том, как должна работать размерность. Но вот для фрактальных кривых такая размерность дает неожиданные результаты: оказывается, что размерность Минковского кривой Коха равна ^{ln 4}/_{ln 3}, что примерно равно 1.26185950714 — то есть она как бы уже не совсем прямая, но и не фигура с площадью, как квадрат.

Фрактальных размерностей много — в том числе у вашего покорного слуги есть кое-какие. В них немало нюансов: какие-то из них легче вычисляются на непосредственных примерах, для каких-то методика вычисления по меньшей мере не очевидна, некоторые дают ответы на одни вопросы, некоторые — на другие. В целом это один из основных методов в данной области — использование метрических характеристик сложных объектов для изучения вопросов, связанных с геометрией кривой, для решения тех или иных задач, на которые она (геометрия) влияет.

В математике часто работают не столько с фракталами, сколько с неспрямляемыми кривыми — широким классом кривых (включающим фракталы), которые объединены тем свойством, что при попытке измерить их длину с помощью ломанной из маленьких (в пределе — бесконечно маленьких) отрезков мы не получим конечное число.

Мы знаем этот фокус из школы: чтобы измерить длину окружности, к ней рекомендовалось приложить нитку или (что то же самое) приблизить ее вписанным правильным многоугольником. Когда мы попробуем приложить нитку к любому из отрезков кривой Коха на каком-то шаге, на следующем шаге отрезок эту нитку порвет «выступившим» углом. Даже если мы возьмем отрезок поменьше, рано или поздно это произойдет и с ним. В классе неспрямляемых кривых есть огромное количество других удивительных «зверей», которые, не являясь самоподобными, обладают этим свойством.

Еще один предварительный факт. Фракталы впоследствии получили огромное число приложений — от компьютерной графики до экологии, от радиоэлектроники до сжатия изображений, от медицины до искусства. Однако поначалу в математическом и в целом в научном сообществе фракталам сопротивлялись. Все эти странные, случайные формы с контринтуитивными свойствами вызывали дискомфорт у людей, привыкших либо работать в абстракциях, либо иметь дело с привычными, спрямляемыми формами. Их даже называли (а иногда и сейчас называют, хотя уже не с той долей негатива) «монстрами».

Наша статья посвящена одному из их применений, которое очень хорошо иллюстрирует тезис о том, что если неспрямляемые кривые и являются монстрами, то стоит признать, что мы полностью ими окружены и уйти от них некуда. Более того, хотя «фрактальный бум» уже прошел, есть еще области, где связанные с фракталами результаты не только применяются, но и могут дать ответы на новые вопросы.

1. Явление «вязких пальцев»

Явление «вязких пальцев» могли заметить многие, но часто его игнорируют или воспринимают как нечто обычное. Однако нередко бывает так, что стоит начать задавать себе вопросы о чем-то привычном, как тут же вырастает целая область для работы.

Не раз его могли наблюдать, например, люди, которые рисуют красками. Если положить грязную влажную кисть на бумагу (особенно хорошо это будет работать с пористой бумагой и достаточно большим количеством воды на кисти) и забыть о ней на некоторое время, то можно заметить, что окрашенное пятно имеет неровные границы. Точнее, обычно в начале пятно имеет примерно круглые или овальные очертания, но затем из него начинают вытягиваться «пальцы» — тонкие и длинные, часто кривые отростки, которые, если жидкости много, как будто наперегонки друг с другом двигаются из центра пятна, а иногда и ветвятся.

В целом явление «вязких пальцев» можно наблюдать в двух основных ситуациях:1) при протекании жидкости под давлением через пористую среду;2) при протекании менее вязкой жидкости через более вязкую при условии, что они не смешиваются.

Для точности высказывания, строго говоря, вместо слова «жидкость» следует использовать слово «среда» — феномен «вязких пальцев» можно наблюдать и на газах.

Первый случай уже проиллюстрирован примером с бумагой и кистью. Конечно, могут быть и другие. Мой личный пример связан с тем, что детство мое выпало на голодные для университетских сотрудников 90-е, когда ради небольшой экономии и для большей уверенности в себе продукты закупались или добывались сразу оптом. У нас в семье, например, обычно стоял мешок с сахаром, употребляемым как в чистом виде, так и для всевозможных домашних заготовок. Так вот, уже тогда я заметил, что если что-то контрастное и засыхающее пролить в этот мешок (мы не станем развивать эту тему), то небольшое количество жидкости застывает на поверхности, а большая ее часть образует длинные и разветвленные, древовидной формы фигуры. Это тогда удивляло меня: казалось бы, при большем количестве жидкости должна была равномерно увеличиваться толщина корки на сахаре без каких-либо аномалий.

Второй пример хорошо виден на материалах, созданных мной с моей соавторкой и медиахудожницей eye_eye арт-объектов для творческой лаборатории Таткульт и галереи «На Каширке» в рамках выставки «Частоты».

Сами арт-объекты несколько отличались по композиции и содержанию, однако нас сейчас волнует в основном их техническая часть, а именно так называемая ячейка Хеле-Шоу и всё, что происходит в ней. Ячейка Хеле-Шоу — это два плоских стекла с тонким зазором между ними. В этом зазоре располагается вязкая среда — в нашем случае это специально подобранная окрашенная жидкость. Кстати, ее подбор был результатом долгой серии экспериментов — не подойдут ни слишком вязкие жидкости, ни слишком жидкие, ни слишком стойкие или слабые красители, поэтому раскрывать секретов я не стану, скажу лишь, что эта вязкая жидкость хорошо знакома практически всем людям моего возраста и старше. В центр верхнего стекла мы устанавливаем систему для подачи воздуха, с помощью нее через специальный шланг будет вдыхать и затем вытягивать воздух своим дыханием посетитель — воздух выступает в качестве второй, менее вязкой среды.

Понаблюдаем немного за картинами, которые возникают в ходе процесса. Интересно, что картины не повторяются, каждый раз мы получаем новый древовидный объект.

Нетрудно заметить, что «пальцы» имеют фрактальную форму — центральный палец делится на меньшие, они на еще меньшие и т. д. Мы вернемся к этому дальше.

Концепция инсталляции — дихотомия хаоса и порядка, предсказуемого состояния и неконтролируемого. Взаимодействие человека с изменчивым миром через организованные процессы, такие как дыхание. Дыхание ритмично, понятно и регулярно. В концепции нашей инсталляции дыхание выражено как устойчивая система, характеризующая собой порядок.

Мир вокруг нас — неустойчивый, непостоянный, хаотичный. Для демонстрации этого непостоянства мы используем феномен «вязких пальцев».

Подробнее об арт-объекте можно почитать тут.

Наполнение и ориентация ячейки Хеле-Шоу могут быть и другими. Например, можно сделать вертикальную ячейку и заполнить ее стеклянными шариками для имитации пористой среды, а затем залить в нее сверху контрастную жидкость. Кроме того, можно сделать объемный аналог ячейки — набить тех же стеклянных шариков или гранул в колбу или банку и наблюдать за течением жидкости по ним. Результат будет приблизительно тот же: вместо равномерного фронта жидкости мы увидим вытянутые древовидные отростки.

2. Как можно воссоздать в домашних условиях

Мы провели для вас несколько экспериментов из подручных средств, на которых неплохо видно явление. Первый эксперимент — собственно, цветное пятно. Использовалась разбавленная водой акриловая краска, беличья кисть и разные пористые подложки. Исходно это был лист бумаги А4 для принтеров, и здесь эффект виден не слишком хорошо, однако всё же заметно, что более бледные границы распространения пятна имеют характерную причудливую форму (и это не брызги краски при падении на бумагу — тогда бы они были того же цвета, что и пятно).

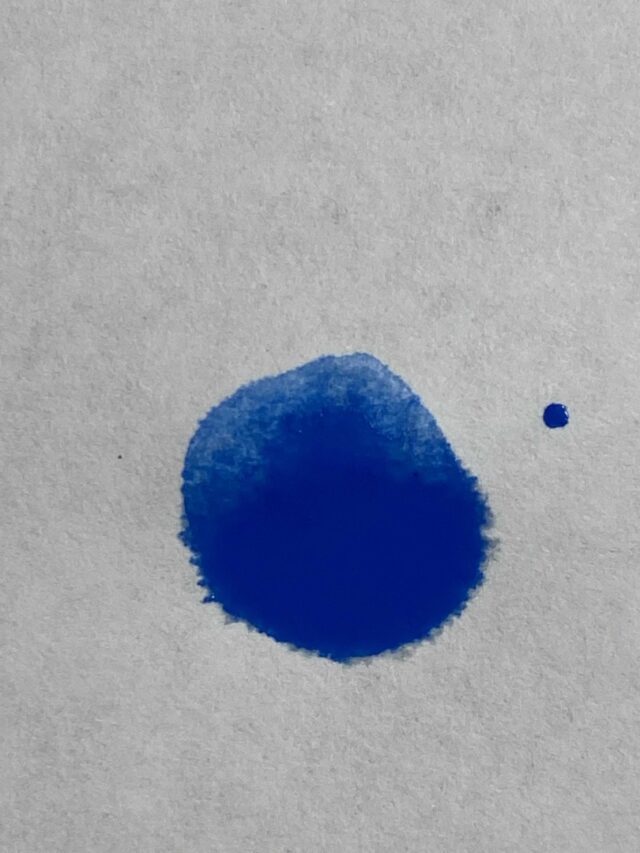
Гораздо лучше картинка вышла при использовании более проницаемой и более пористой структуры — ватного диска. Здесь ситуация интересна не только тем, что получились характерные древовидные «пальцы», но и тем, что диск, будучи не совсем плоским, обнаруживает спрятанный в своей глубине «палец». Здесь тоже можно усмотреть некую фрактальную, древовидную структуру.

Наконец, с обратной стороной картонного костера от пива «Жигулевское» эксперимент не удается целиком и полностью — слишком плотный картон не впитывает насыщенную краской воду, а значит, и «пальцев» не дает.

Второй эксперимент, который мы для вас провели, чуть сложнее. В нем мы впрыскивали окрашенную воду в сахар, вертикально зажатый между двух слоев пластика, отрезанного от упаковки «Кухни на районе». Поначалу кажется, что ничего интересного не происходит, за исключением небольших «пальцев» по краям пятна. Однако затем мы видим длинный палец справа, совсем не там, где осуществляется впрыскивание жидкости.

Много эстетически близких явлений можно наблюдать у современного художника Stefan Visan здесь:

View this post on Instagram

A post shared by Stefan Visan (@visanstefan)

3. Попытка разобраться на пальцах

Попробуем объяснить в очень упрощенном виде, что же происходит в зоне формирования «пальца» на примере воздушного пузыря в середине ячейки Хеле-Шоу с вязкой средой. Поначалу в зоне ввода воздуха в самом деле формируется достаточно круглый пузырек. Если мы прекратим вдыхать воздух, таким он и останется. Однако если мы продолжим подачу воздуха, то пузырю нужно будет куда-то расширяться. Среда никогда не является абсолютно однородной, это же относится к шероховатости верхнего и нижнего стекла, гравитации — в целом ко всему, что может повлиять на движение воздуха. Разумеется, пузырь будет в первую очередь расширяться в ту сторону, в которую это будет легче сделать, поэтому сначала на пузыре образуется небольшой бугорок в том направлении, где неоднородность условий играет воздуху на руку. Затем обнаруживается, что в силу возникшей асимметрии пузыря двигаться в том же направлении энергетически выгодно — давление в направлении возникшего бугорка выше и именно туда устремляется больше воздуха. Таким образом, «палец» растет дальше. Затем он встречает новую неоднородность, в которой либо искривляется, либо выпускает новый «палец».

4. Немного формул

Для простоты начнем с ячейки Хеле-Шоу — двух слоев стекла с расстоянием b между ними. Между стеклами закачана более вязкая жидкость. Если ячейка установлена горизонтально, то менее вязкая жидкость впрыскивается в центре ячейки, если вертикально, то мы считаем, что она поступает снизу и выталкивает более вязкую жидкость вверх. Скорость (средняя по толщине зазора между стеклами) течения U в такой ячейке имеет вид:

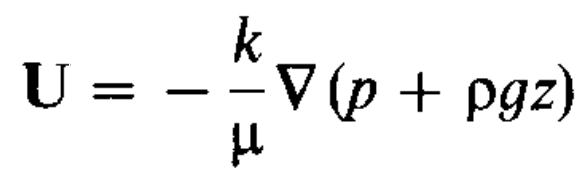
где p — давление, — плотность, z — координата на вертикальной оси, g — составляющая ускорения свободного падения вдоль вертикальной оси, — вязкость жидкости, k — проницаемость ячейки (в описываемом случае она равна b²/₁₂). В случае горизонтально лежащей ячейки, конечно, всё второе слагаемое в скобках обнуляется.

Для несжимаемых жидкостей (а такими можно с достаточной точностью считать все описываемые нами здесь случаи) это уравнение трансформируется в уравнение Лапласа, описывающее, в частности, потенциал в задачах электростатики и диффузии. Конечно, кроме уравнения выше, существуют еще так называемые граничные условия — например, это могут быть заданные значения давления в концах ячейки и нулевая скорость всюду, где жидкость соприкасается со стенками.

Если в вертикальной ячейке одна жидкость вытесняет вверх другую (будем считать, что мы впрыскиваем одну жидкость в точке с z (вертикальной координатой) = — ∞ и откачиваем вторую в точке с z = + ∞). Когда мы начнем впрыскивать жидкость, граница раздела будет двигаться с постоянной скоростью U = (0, 0, U). Однако если вязкость первой жидкости ниже вязкости второй, то граница их раздела становится неустойчивой. Это означает, что возникающие возмущения (вызванные неоднородностью среды, внешними источниками, чем-то еще) могут вызвать резкую перемену картины — возможно, необратимую.

Собственно, наблюдая за вытеснением нефти водой в пористой среде, Энгельбертс и Клинкенберг и предложили термин «образование вязких пальцев».

Попробуем отследить, как двигается и меняет форму граница раздела двух жидкостей. Пусть на конечной длине ячейки от z = 0 до z = L существует разность давлений от p₁ до p₂. Вязкостью вытесняющей среды мы пренебрегаем и заранее предположим, что «пальцы» будут двигаться в ту же сторону, что и фронт раздела, как бы обгоняя его, — тогда давление на конце «пальца» также p₁. Тогда наибольший градиент давления будет на конце «пальца» (в точке с координатой z) и будет равен

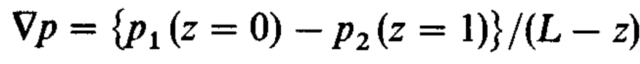
Для исследования неустойчивости мы накладываем на нашу картину синусоидальное возмущение с длиной волны . Для устойчивого фронта раздела скорость нарастания ниже нуля, и это означает, что возмущение гасится со временем. Для неустойчивого фронта скорость нарастания возмущения положительна и оно нарастает экспоненциально.

Решая с учетом возмущения уравнение на скорость (с которого мы начинали) и его следствия, можно получить любопытный результат: существует (и может быть вычислена из исходных данных задачи) так называемая критическая длина волны, фронт вытеснения оказывается неустойчивым относительно возмущений с длиной волны более критической. Если же длина волны возмущения менее критической, то поверхностное натяжение на границе раздела стабилизирует возмущение. Фронт будет неустойчив при всех возмущениях с длинами волн больше критической, но наибольшую скорость нарастания будут иметь возмущения с длиной волны, равной 3от критической длины волны, — именно они будут определять динамику фронта. Следовательно, можно ожидать, что в ячейке Хеле-Шоу будут возникать «пальцы» с характерным периодом m. В горизонтальной ячейке этот период будет равен

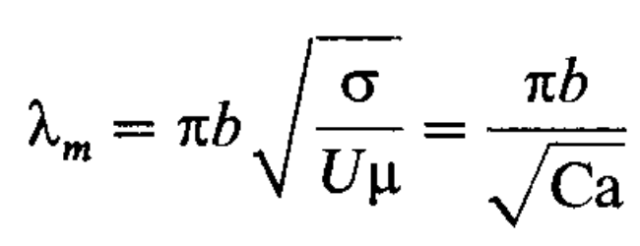
где — поверхностное натяжение на границе сред, Ca — капиллярное число, равное отношению вязких сил к капиллярным силам.

В заключение приведем еще несколько любопытных экспериментов и их результаты.

Саффмен и Тейлор вытесняли воздухом глицерин в вертикальной ячейке сверху вниз. Обратите внимание, что на поздних этапах большие «пальцы» тормозят рост своих соседей.

Источник: Saffman P.G., Taylor G.I. The Penetration of a fluid into a medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. Lond., 245, 312–329, 1958

Они же экспериментировали с водно-глицериновым раствором, также сверху вытесняющим нефть:

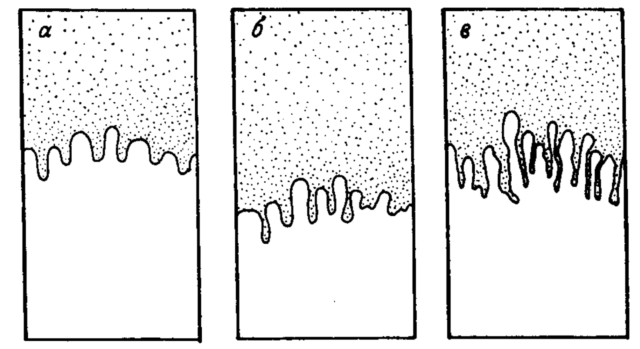
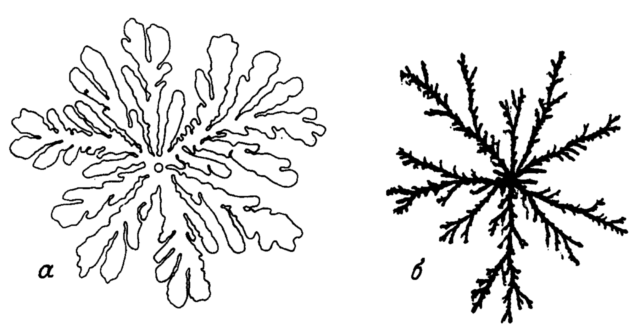
Ниттман, Даккорд и Стэнли использовали неньютоновскую жидкость — раствор склероглютана в воде — и, вытесняя его водой, получили очень узкие «пальцы». На рисунках ниже они представлены в сравнении с «пальцами», получившимися при вытеснении глицерина водой. Выглядит довольно похоже на картинки из арт-объекта, правда? На результатах этого эксперимента нетрудно заметить фрактальную структуру «пальцев»: оказывается, что их размерность Минковского равна 1.70 ±0.05.

Источник: Måløy K.J., Feder J., Jøssang T. Radial viscous fingering in a Hele-Shaw cell. Report Series, Cooperative Phenomena Project, Department of Physics, University of Oslo, 85–9, 1–15, 1985

Приведенные выше формулы неплохо описывают процесс возникновения «вязких пальцев» при вытеснении одной жидкостью другой. Однако их поведение в пористой среде не так предсказуемо — дело в том, что кроме собственно динамики жидкости в дело вступает случайность, вызванная переменным размером пор.

Здесь включаются в процесс метрические размерности. С одной стороны, исходя из геометрии пор, можно было бы попробовать вычислить проницаемость из первой формулы в этом разделе — очевидно, она не такая простая, как в случае обычной ячейки Хеле-Шоу, — и затем, основываясь на ней, получить какие-то предположения о динамике жидкости. С другой, фрактальные размерности фигур, образуемых движущейся жидкостью, могут дать представление о геометрии пор.

5. Практическое применение

Конечно, из того, что «вязкие пальцы» — красивое и интересное явление, не следует, что нужно его немедленно изучать. Как часто бывает, здесь человеческий интерес подстегивается, главным образом, большими деньгами.

Основная область приложения результатов, связанных с «вязкими пальцами», — добыча нефти. Дело в том, что любые, даже чисто инженерные задачи, связанные с нефтяной отраслью, стоят очень дорого. Если мы неверно спрогнозируем объемы нефтяных запасов, если наши действия отсрочат начало добычи или вовсе остановят производство, мы не только потратим массу ресурсов, что едва ли не важнее — мы ударим по биржам, в отдельных случаях экономики целых регионов могут оказаться под угрозой.

Чтобы этого избежать, нужно понимать динамику нефтяных объемов до того, как мы начнем что-то делать. Первая история здесь возникает в связи со способом добычи нефти, основанным на закачивании под нее воды. Вода, конечно, гораздо менее вязкая жидкость, чем нефть, и как раз за счет формирования «пальцев» может оказаться, что нефть (будучи более легкой) не идет к нам наверх сплошным фронтом. Вместо этого образуются длинные водяные «пальцы» — в гипотетической ситуации мы вообще можем получить обратно ту же воду, которую закачиваем вниз через длинный водяной палец. Вторая проблема, нуждающаяся здесь в проработке, — движение жидкости по пористым структурам. Иногда нефть (впрочем, не только она) под землей за счет давления проходит сквозь настолько плотные породы, что срез их нам показался бы полированным гладким камнем. Как себя поведет поток жидкости в такой среде, не возникнет ли «пальцев», уводящих его куда-то в сторону, — это всё вопросы, на которые хорошо бы знать ответ не только перед бурением скважины, но и перед тем, как объявлять о нахождении очередного месторождения. Ошибки здесь могут стоить очень дорого. Кроме того, интерес образование «вязких пальцев» вызывает и в гидродинамике, и в физике пористых сред.

6. В качестве заключения

Есть известное высказывание: «Мир полон великих светочей и таинств, но человек закрывает их от себя одной маленькой рукой». Оно хорошо подходит для описания нашей истории. Можно сопротивляться и не замечать новое, можно перемещать целые области исследований в «серую зону», считать их непрестижными и неинтересными, а их структуры — редким исключением из правил, некой занятной экзотикой, которой приличному человеку заниматься не подобает. Однако иногда такое отношение разбивается о действительность. Пример с «пальцами» неплохо иллюстрирует то, что сложные, не характерные для традиционной геометрии формы не являются редкой диковинкой, а, наоборот, окружают нас. Строго говоря, всё с точностью до наоборот — «хорошие», спрямляемые кривые являются некими отдельными исключениями из страшного и бушующего, но реального мира неспрямляемости.

P.S. Смартфон, с которого вы, вероятно, читаете этот текст, помещается в ваш карман тоже благодаря фрактальной форме антенны — без нее бы пришлось делать по антенне на каждую принимаемую длину волны, и он был бы больше похож на ежа.

Нефть, искусство и «вязкие пальцы», или Несколько историй о неспрямляемых кривых