«Общество еще не готово к неевклидовой геометрии», или Почему Николай Лобачевский так и не получил научного признания при жизни
Николай Иванович Лобачевский (1792–1856) — один из научных героев России, его именем назван университет и улицы в нескольких городах, его портреты висят в школьных кабинетах математики. Именно его называют первооткрывателем неевклидовой геометрии. Тем удивительнее, что современники считали Лобачевского ученым-фриком. Научного признания при жизни он так и не увидел, а умер в нищете. Биографы даже окрестили его Коперником или Колумбом геометрии. О том, как российский математик оказался в череде ученых, чьи идеи опередили время, рассказывает Андрей Вдовенко.
Путь первооткрывателя
Будущий создатель неевклидовой геометрии родился в Нижнем Новгороде в 1792 году. Он рос с двумя братьями без отца. Тот, мелкий чиновник-геодезист родом из крепостных, рано скончался. Мать Лобачевского была женщиной энергичной и смогла дать сыновьям хорошее образование за казенный счет. Все трое Лобачевских окончили единственную на тот момент в Поволжье и Сибири Казанскую гимназию и поступили в недавно открывшийся на ее основе Императорский университет — тогда самый восточный в России.
Здесь Лобачевский сделал стремительную карьеру. В 19 лет он уже читал лекции, в 21 год стал адъюнктом (доцентом по сегодняшним меркам), в 23 — профессором, в 28 — деканом физико-математического факультета, а в 34 — ректором. Ректоров в те времена избирали университетские советы; за Лобачевского ученые мужи голосовали шесть раз.

Трудно назвать раннюю жизнь Лобачевского легкой. Обучаясь за казенный счет, он жил практически в казарменных условиях: не мог свободно покидать гимназию и университет и видеться даже с матерью, обязан был следовать строгому расписанию и дисциплине. Тем не менее юноша рос свободолюбивым и упрямым.
Например, любил пошалить. Его имя 33 раза была вписано в специальную книгу нарушений — кондуит. Лобачевский катался на корове, на спор перепрыгивал тучного профессора Никольского, ходил на маскарады, несмотря на запрет, пускал ракету в университетском дворе. За последний проступок он отсидел трое суток в карцере — тогда это была такая воспитательная мера. А за участие в маскарадах Лобачевского чуть не отчислили и не отправили в солдаты. Позднее, уже будучи ректором, он не судил провинившихся студентов строго и даже спасал некоторых. Например, студента Криницына, который разбил окно в церкви и мог быть отправлен в солдаты, а в итоге окончил университет и получил хорошую должность в Сибири. Незадолго до смерти Лобачевского Криницын навестил своего спасителя и горячо поблагодарил его.
Свободный и упрямый нрав Лобачевский сохранил на протяжении всей жизни, несмотря на многолетнюю административную службу. Так, уже работая в Казанском университете, молодой преподаватель отказался произнести актовую речь о важности христианского воспитания. И это несмотря на опасность попасть в жернова консервативной реакции.
Наука не была единственным делом жизни Лобачевского. За 19 лет на посту ректора он превратил Казанский университет из захолустной высшей школы, где преподавателей было едва ли не больше, чем студентов, в один из лучших вузов империи. Обладая кипучей энергией и неиссякаемой работоспособностью, он брал на себя самые разные обязанности: от наведения порядка в библиотеке до строительства университетских зданий.
Лобачевский решительно действовал во время эпидемии холеры (1830) и крупного пожара (1842) в Казани. Труды его отмечал император — Лобачевский был кавалером нескольких государственных орденов и получил потомственное дворянство. А еще он читал много лекций: все разделы математики, физику и астрономию. По воспоминаниям студентов, Лобачевский был хорошим, хоть и требовательным преподавателем.

Упорная евклидова геометрия и ее пятый постулат
Геометрия как наука сложилась давно — несколько тысячелетий назад. Знания о пространстве начали собирать еще представители древнейших цивилизаций: египетской, вавилонской, индийской, эгейской (крито-микенской). Они, размечая поля и возводя здания, обнаружили множество геометрических правил. В III веке до н. э. древнегреческий ученый Евклид обобщил все известные на тот момент сведения о геометрии в труде «Начала». Именно на основе «Начал» в дальнейшем геометрия веками развивалась как наука, а сам труд стал образцом научного изложения.
Евклид установил пять постулатов и девять аксиом. Почти два тысячелетия на них строилась вся геометрия — евклидова геометрия. Вот эти пять постулатов:
- Через две точки можно провести прямую.
- Отрезок прямой можно неограниченно продолжить.
- Данным радиусом из данной точки можно провести окружность.
- Все прямые углы равны между собой.
- На плоскости через точку, лежащую вне прямой, проходит только одна параллельная, то есть не пересекающаяся с первой прямой.
Заметно, что последний постулат Евклида сложнее остальных и менее «интуитивен». Особенно это бросается в глаза, если обратиться не к более поздней формулировке, представленной выше, а к оригиналу Евклида. Тот говорил, что если сумма углов при пересечении двух прямых третьей будет меньше 180°, то они непременно пересекутся.
Пятый постулат очень важен, так как из него выводится доказательство того, что сумма углов треугольника равна 180° или, например, вывод о существовании прямоугольников. При этом истинность пятого постулата недоказуема на чертеже: бесконечно вести две параллельные прямые попросту невозможно. На то, что аксиома Евклида больше похожа на теорему, обратили внимание еще в Античности.
Поэтому ученые веками пытались найти доказательство пятого постулата. Этим занимались античные мыслители Посидоний (II— I века до н. э.), Клавдий Птолемей (II век н. э.) и неоплатоник Прокл (410–485). Затем задачу пытались решить арабские исследователи Аль-Аббас аль-Джаухари и Сабит ибн Курра (оба — IX век), Омар Хайям (1048–1131) и Насир ад-Дин ат-Туси (1201–1274). Потом за пятый постулат взялись европейцы: Леви бен Гершома (1288–1344), иезуит Христофор Клавий (1537–1612), гениальный английский математик-самоучка Джон Валлис (1616–1703), французы Алексис Клеро (1713–1765) и Адриен-Мари Лежандр (1752–1833), русский академик Семен Гурьев (1766–1813) и др.
Но никому из них не удалось продвинуться дальше Евклида. Чаще всего они просто формулировали его пятый постулат другими словами или «доказывали» его положением, вытекающим из него самого.
Ближе всех к решению загадки пятого постулата были итальянец Джироламо Саккери (1667–1733) и немец Иоганн Генрих Ламберт (1728–1777). Они первыми попытались пойти от противного, то есть признать саму возможность существования геометрии, отличной от евклидовой. Оба взяли за основу несовместимое с пятым постулатом положение о треугольнике, сумма углов которого меньше 180°. Саккери пришел к выводу, что такая фигура не может существовать. Ламберт заключил, что всё-таки может, но не нашел тому доказательств и ограничился выводом о том, что пятый постулат в принципе недоказуем. Труды обоих мыслителей прошли практически незамеченными среди современников.
Открытие, которого никто не ждал
В начале XIX века пятый постулат вновь стал популярен среди математиков. Попытался его доказать в 1810–1820-е годы и молодой Николай Лобачевский. Когда у него также не получилось, он тоже решил пойти от противного. Лобачевский придумал полностью противоположный Евклиду постулат: «На плоскости через точку, лежащую вне прямой, проходит не менее двух не пересекающих ее других прямых». Исходя из этого условия, он попытался найти доказательство своему постулату и в итоге нашел.
На тот момент Лобачевский был не единственным математиком, приблизившимся к открытию неевклидовой геометрии. Параллельно и независимо от него схожие идеи развивали Карл Фридрих Гаусс (1777–1855), Фердинанд Карл Швейкарт (1780–1857), Франц Адольф Тауринус (1794–1874) и Янош Бойяи (1802–1860). Последний считается первооткрывателем неевклидовой геометрии наряду с российским ученым. Но именно Лобачевский первым опубликовал труд, который бросил вызов всем бытовавшим до этого в математике представлениям. Кроме того, он единственный активно продолжил работать над неевклидовой геометрией и печатать труды по ней, несмотря на обрушившуюся критику.
В литературе часто относят появление геометрии Лобачевского (первой из неевклидовых) к 1826 году. Тогда профессор Лобачевский на заседании физико-математического факультета прочитал доклад «Сжатое изложение основ геометрии со строгим доказательством теоремы о параллельных». Но сам текст доклада не сохранился, а отзыв, который на него должны были сделать рецензенты, так и не появился.
Поэтому с абсолютной уверенностью временем появления неевклидовой геометрии можно считать 1829–1830 годы, когда Лобачевский опубликовал труд «О началах геометрии». Работа вышла в «Казанском вестнике» — журнале Казанского университета.
Главный вывод Лобачевского: евклидова геометрия не абсолютна. Она не всегда способна точно отражать свойства пространства, так как возможно существование пространства, в котором сумма углов треугольника меньше 180°. Поэтому в «воображаемой», как ее называл сам Лобачевский, геометрии выполнялись все аксиомы Евклида, кроме пятой.
«Напрасное старание [доказать пятый постулат] со времен Евклида, в протяжении двух тысяч лет, заставило меня подозревать, что в самых понятиях еще не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения».
Николай Лобачевский. Цит. по: Володаров В.П., «Непризнанный при жизни гений», «Вестник РАН», № 12, 1992 год
Эти идеи переворачивали с ног на голову господствовавшие два тысячелетия истины. Даже понять то, о чем говорил Лобачевский, на тот момент могли далеко не многие. Публикация такого труда была очень дерзким поступком, настоящим вызовом для геометров.
Тем не менее два года никто открытия Лобачевского как будто не замечал, пока в 1832 году текст его работы не был направлен в Петербургскую академию наук. В столице труд Лобачевского не оценили: одни ничего в нем не поняли, другие удивлялись чрезмерной сложности изложения, третьи попросту насмехались.
«Воображаемая» геометрия подверглась жестокой, язвительной и необоснованной критике. Словно танком по ней прошелся академик, великий ученый Михаил Остроградский — главный математик страны в ту эпоху. Он заявил, что ничего не понял в труде Лобачевского и нашел в нем ошибку в интегралах. «Книга г-на Лобачевского опорочена ошибкой, небрежно изложена и, следовательно, не заслуживает внимания Академии», — писал он. На самом деле, Остроградский ошибался сам.
Лобачевского обвиняли в высокомерии, чудовищной гордости, тщеславии и корысти. Апогеем травли стала статья 1834 года в реакционном журнале «Сын Отечества». Автор (или авторы) публикации, скрывшийся за псевдонимом С.С., обливал математика грязью в развязном тоне, характерном для этого издания:
«Даже трудно было бы понять и то, каким образом г. Лобачевский из самой легкой и самой ясной в математике науки, какова геометрия, мог сделать такое тяжелое, такое темное и непроницаемое учение, если бы сам он отчасти не надоумил нас, сказав, что его геометрия отлична от употребительной, которой все мы учились, и которой, вероятно, уж разучиться не можем, и есть только воображаемая. Да, теперь всё очень понятно. Чего не может представить воображение, особливо живое и вместе уродливое? Почему не вообразить, например, черное белым, круглое четыреугольным, сумму всех углов в прямолинейном треугольнике меньшею двух прямых и один и тот же определенный интеграл равным то π/4, то ∞? <...>
Как можно подумать, чтобы г. Лобачевский, ординарный профессор математики написал с какой-нибудь серьезной целью книгу, которая немного бы принесла чести и последнему школьному учителю! Если не ученость, то, по крайней мере, здравый смысл должен иметь каждый учитель, а в новой геометрии нередко недостает и сего последнего.
Соображая всё сие, с большою вероятностью заключаю, что истинная цель, для которой г. Лобачевский сочинил и издал свою геометрию, есть просто шутка или лучше сатира на ученых-математиков, а может быть и вообще на ученых сочинителей настоящего времени <...>
Но сознавая всю цену сочинения г. Лобачевского, я не могу однако ж не попенять ему за то, что он, не дав своей книге надлежащего заглавия, заставил нас долго думать понапрасну. Почему бы вместо заглавия «О началах геометрии» не написать, например, «Сатира на геометрии», «Карикатура на геометрии», или что-нибудь подобное? Тогда бы всякий с первого взгляда видел, что это за книга, и автор избежал бы множества невыгодных для него толков и суждений. Хорошо, что мне удалось проникнуть настоящую цель, с которою написана эта книга, — а то, Бог знает, что́ бы и я об ней и ее авторе думал. Теперь же думаю и даже уверен, что почтенный автор почтет себя весьма мне обязанным за то, что я показал истинную точку зрения, с которой должно смотреть на его сочинение«.
«О началах Геометрии, соч. Г. Лобачевского», «Сын Отечества», т. XLV, 1834 год
Автор пасквиля на Лобачевского либо не понял «воображаемую» геометрию, либо намеренно исказил ее смысл. Так, он считал новую геометрию бесполезной при реальных измерениях, созданной лишь для того, чтобы «опровергнуть» Евклида. Лобачевский же говорил абсолютно противоположное. Он считал, что математика должна быть не абстрактной, а максимально приближенной к явлениям реального мира. А «воображаемая» геометрия, по его мнению, могла быть полезной в астрономических расчетах и для аналитики. Евклидову же геометрию он вовсе не отрицал, а считал ее частным критическим случаем более общей и сложной геометрии.
Но, судя по всему, Лобачевского действительно никто не понял. В своих трудах ученый придерживался крайне скупой манеры изложения, не всегда подтверждая свои мысли вычислениями и примерами. Вот как о нем вспоминал студент Петр Перцов:
«В своих чтениях Николай Иванович развивал всегда подробно каждую формулу, в противоположность своим печатным трудам, где он часто просто говорит: „от такой-то формулы переходим к такой-то“, а как происходит этот переход — не разъясняет, чем сильно затрудняется усвоение вопроса».
Цит. по: Модзалевский Л.Б. «Материалы для биографии Н.И. Лобачевского»
На непонятность изложения сетовал и критик из «Сына Отечества». Он даже приводил цитаты самого Лобачевского. Например:
«Когда два тела А, В касаются каждое третьего С в точке, тогда относительное положение двух точек или так называемое расстояние их друг от друга, всякий раз будет определено, как скоро А и В соединены телом D, неприкосновенным к С, хотя бы при этом в А, В, D происходили перемены отделением, или присоединением новых частей, неприкосновенных к С, или те изменения в А и В, которые дозволяются в сем роде прикосновения А, В с С. Так циркуль служит для назначения расстояний».
Так или иначе, возможности ответить редакция «Сына Отечества» Лобачевскому не предоставила. Притом что публикации в этом издании были равносильны политическому доносу. Из-за нападок Лобачевский чуть не лишился ректорского поста на очередных выборах. А петербургские профессора так и не дали ему защитить докторскую диссертацию.
Упорный Лобачевский
Несмотря на выпады критиков, Лобачевский был непреклонен и не только не отказывался от своей «воображаемой» геометрии, но и продолжал печатать свои труды по ней. В 1835 году в «Ученых записках Императорского Казанского университета» (бывшем «Казанском вестнике») вышла его «Воображаемая геометрия», а в 1835–1838-м — «Новые начала геометрии с полной теорией параллельных».

Не найдя соратников в своей стране, Лобачевский опубликовал «Воображаемую геометрию» на французском языке в авторитетном журнале немецкого математика и архитектора Августа Леопольда Крелле. А в 1840 году на немецком вышла его небольшая книга «Геометрические исследования по теории параллельных». О трудах казанского профессора узнали в Европе, но не то чтобы они произвели там фурор.
Среди тех, кому на глаза попались «Геометрические исследования...», был и Карл Фридрих Гаусс — создатель теории чисел и поверхностей, а также понятия полной кривизны, «король математиков», или «принцепс математикорум», как его называли. Знаменитый немецкий ученый высоко оценил изыскания Лобачевского, заметив, что и сам много мыслил в этом направлении. Вот что он говорил о работе Лобачевского в письме астроному Генриху Шумахеру 1846 года:
«Вы знаете, что уже 54 года (с 1792 года) я разделяю те же взгляды (с некоторым развитием их, о котором не хочу здесь упоминать); таким образом, я не нашел для себя в сочинении Лобачевского ничего фактически нового. Но в развитии предмета автор следовал не по тому пути, по которому шел я сам; оно выполнено Лобачевским мастерски, в истинно геометрическом духе. Я считаю себя обязанным обратить Ваше внимание на это сочинение, которое, наверное, доставит Вам совершенно исключительное наслаждение».
Вот только открыто об этом Гаусс не сказал. Он признавал «воображаемую» геометрию только в дневниках и личной переписке на условиях анонимности. Ученый считал, что общество еще не готово к неевклидовой геометрии, и боялся криков «беотийцев», то есть невежд. Поэтому он предпочел быть никак не связанным с громким, но вызывавшим столько споров открытием. Вот как он сам об этом говорил в письмах венгерскому математику, отцу Яноша Бойяи Фаркашу Бойяи и немецкому математику Фридриху Вильгельму Бесселю:
«Я имел намерение о своей собственной работе, кое-что из которой я теперь нанес на бумагу, при жизни ничего не публиковать. Большинство людей совершенно не имеет правильного понятия о том, о чем здесь идет речь; я встретил только очень немногих людей, которые с особенным интересом восприняли то, что я им об этом сообщил».
«Вероятно, я еще не скоро смогу обработать свои пространные исследования по этому вопросу, чтобы их можно было опубликовать. Возможно даже, что я не решусь на это во всю свою жизнь, потому что я боюсь крика „беотийцев“, который поднимется, когда я выскажу свои воззрения».
Опасливость, а быть может, и ревность к первенству в научных открытиях Гаусса сыграли дурную шутку с другим первооткрывателем неевклидовой геометрии — венгерским военным инженером Яношем Бойяи. На рубеже 1820–1830-х годов он независимо от Лобачевского пришел к тем же выводам и отправил Гауссу на отзыв свою работу (она была опубликована позже — в 1832 году). Холодный ответ «короля математиков», который заявил, что работает над темой уже 30–35 лет, разозлил Бойяи и расстроил его нервы. А когда Гаусс прислал Бойяи работу Лобачевского, тот и вовсе вышел из равновесия. Он заподозрил коллег в плагиате, пытался опровергнуть их, а по сути и свои собственные, идеи. Так и не вернувшись к нормальному состоянию, он больше не довел ни одного труда до конца. Лобачевский же о существовании Бойяи, судя по всему, так и не узнал.
К казанскому коллеге Гаусс, похоже, был более благосклонен. Именно он рекомендовал принять Лобачевского как одного из лучших математиков России в члены-корреспонденты Геттингенского королевского научного общества. По сути, это было единственное прижизненное признание научных заслуг Николая Ивановича. Поговаривают также, что у Гаусса были почти все сочинения Лобачевского. Но прямо своих симпатий ему немецкий математик так и не высказал.
На родине же Лобачевский за год до смерти стал почетным членом Московского университета. А поддержал его идеи только профессор механики Казанского университета Петр Котельников. В своей речи 1842 года он отметил, что «воображаемую» геометрию рано или поздно ждет признание. Что характерно, в тот же год Остроградский дал новую отповедь трудам Лобачевского по решению некоторых проблем анализа.
И хотя Лобачевского уважали как деятеля высшей школы, о его геометрии, как вспоминал Александр Бутлеров, продолжали говорить «с улыбкою снисходительного отношения к чудаку ученому». Коллеги-соотечественники обходили его труды стороной. Например, профессор Виктор Буняковский, разбирая различные доказательства постулата Евклида о параллельных прямых, даже не упомянул о «воображаемой» геометрии.
Жизнь в неевклидовом пространстве
«Еще вы не в состоянии дать истинной цены словам моим, и не вдруг опытность может вразумить вас. Теперь вступаете вы в свет; новизна и многоразличность впечатлений не дает места размышлениям. Но придет время, когда на блеске настоящего вдруг явится прошедшее с обворожительною прелестию своего туска, подобно нежной затуманенной резьбе на ярком золоте, подобно отраженным предметам в слабом зеркале вод; тогда лета воспитания, лета беззаботной юности всеми невинными удовольствиями предстанут в вашем воспоминании, как образ совершенного счастия, невозвратимо потерянного».
Из речи Н.И. Лобачевского «О важнейших предметах воспитания» по поводу первой годовщины его ректорства
Конец жизни великого ученого и великого ректора Николая Лобачевского был печален: он практически вернулся в ту бедность, в которой родился. В 1846 году Лобачевского сняли с постов ректора и профессора, несмотря на просьбы совета Казанского университета его оставить. Причиной тому могло быть как завинчивание гаек новым министром просвещения Платоном Ширинским-Шихматовым, так и неоднозначная репутация математика в научном сообществе.
Лобачевскому предоставили номинальную должность помощника попечителя учебного округа. За нее ученому даже не платили жалование: Лобачевский получал только сравнительно небольшую профессорскую пенсию. Казенное жилье он с семьей вынужден был покинуть.
К тому моменту финансовые дела первооткрывателя неевклидовой геометрии уже шли неладно, а стали еще хуже. Так, его попытки вводить в вотчине, купленной в долг, новые технологии в условиях крепостничества приносили только убытки. Без жалования Лобачевский стал стремительно разоряться. Дом в Казани и имение жены были проданы за долги. В итоге у детей ученого даже не нашлось средств, чтобы приехать в Казань на празднование столетия со дня рождения отца.
Несмотря на нищету и непонимание коллег, Лобачевский продолжал работать и участвовать в жизни университета, которому отдал всю жизнь. Из-за привычки писать мелким почерком и неумеренности в работе он стал слепнуть, также его мучили приступы потери сознания. Но и это не сломило великого математика: последний труд Лобачевского, «Пангеометрию», его ученики записали под диктовку.

В 1856 году 64-летний Николай Лобачевский скончался от «паралича дыхательного центра». Извещение о выделении ему 1500 рублей, которые ученый попросил на лечение в Москве, пришло всего за 12 дней до смерти. Дожить до вручения серебряной и бронзовой медалей Гаусса, присужденных Геттингенским обществом после смерти «короля математиков», Лобачевскому и вовсе было не суждено.
Однако идеи его продолжили жить. Математик совсем немного не дожил до триумфа неевклидовой геометрии. Уже в 1860-е годы в Германии стали публиковать документы Гаусса. В том числе восторженные отзывы о «воображаемой» геометрии и ее авторе. После этого труды Лобачевского стали обретать популярность, европейские ученые начали их активно переводить, изучать и развивать.
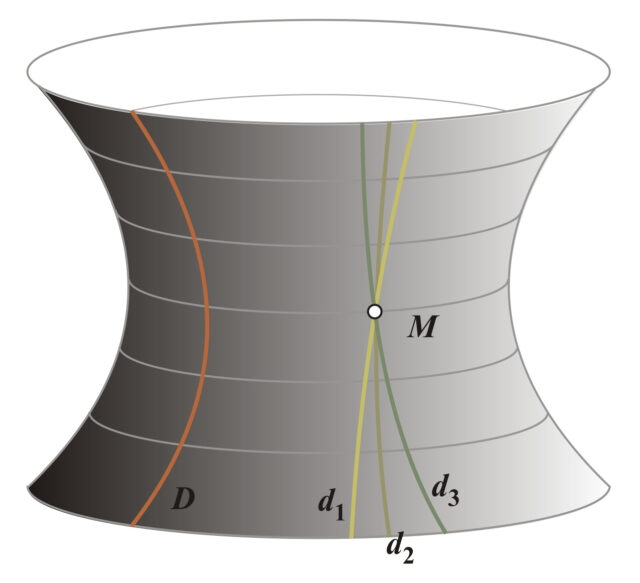
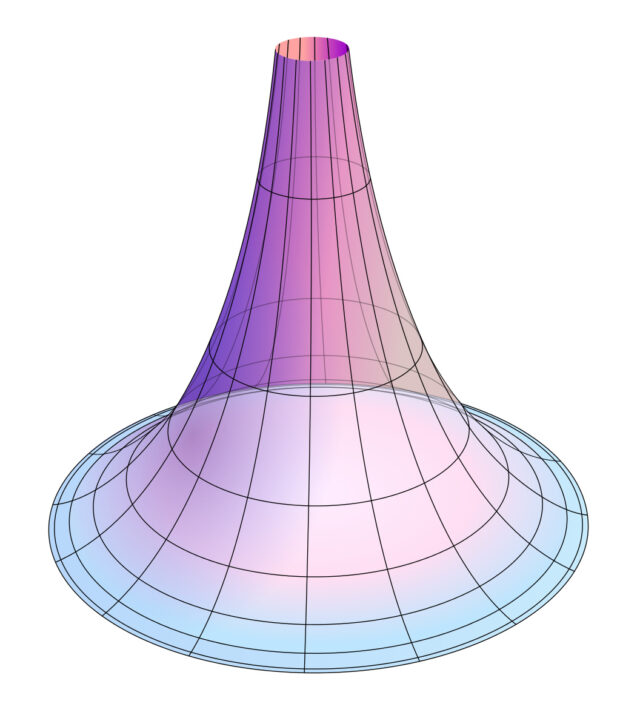
Истинность идей Лобачевского доказал итальянский математик Эудженио Бельтрами в 1868 году. Он смог наглядно показать, что геометрия Лобачевского реализуется на поверхностях с отрицательной кривизной, например на так называемой псевдосфере. В таком пространстве у геодезической, то есть кратчайшей линии, проходящей через две фиксированные точки, может быть множество «параллельных».
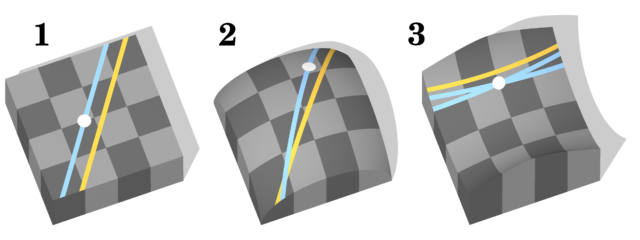
Работы Фердинанда Миндинга, Бернгарда Римана, Уильяма Кингдона Клиффорда, Феликса Клейна и Анри Пуанкаре развили идеи Лобачевского. Оказалось, что неевклидовых геометрий может быть много. Например, в римановой геометрии пространство имеет положительную кривизну, а потому в нем параллельных линий не существует вовсе, а сумма углов треугольника больше 180°.
Открытие неевклидовой геометрии стало большим шагом вперед в физико-математических дисциплинах. Например, существование теории относительности, показавшей, что пространство значительно сложнее того, каким его представлял себе Лобачевский, было бы невозможно без неевклидовой геометрии.
В России же даже среди людей с математическим образованием о Лобачевском знали немногие. Гораздо чаще его имя звучало среди спиритистов, искавших некое пространство четырех измерений.
Читайте также
Память о великом ученом в основном хранили профессора, студенты и выпускники Казанского университета. Видя, как востребован их соотечественник за рубежом, в 1868 году профессор Мариан Ковальский инициировал издание «Полного собрания сочинений Лобачевского по геометрии». Но вышло оно только в 1883–1886 годах. К тому моменту многие работы математика уже были утеряны. Так, когда западные коллеги попросили оригинал «Пангеометрии» Лобачевского для перевода, оказалось, что текст на русском языке большей частью утерян.
То же произошло со многими материалами о жизни ученого. Из-за этого, например, случилась путаница в датах. В итоге первое масштабное торжество в честь Лобачевского — столетие со дня рождения — отмечали в 1893 году, а не в 1892-м. Само празднование юбилея состоялось усилиями Физико-математического общества Казани.
Заслуги Лобачевского наконец признали на родине. Его именем были названы улицы в Казани и Нижнем Новгороде, на доме, где он жил и скончался, повесили мемориальную доску, а возле Казанского университета разбили сквер в его честь. Здесь ученому поставили памятник работы первой российской женщины-скульптора Марии Диллон, который стоит до сих пор.

Деньги на памятник собрали с помощью Комитета для подписки на капитал имени Лобачевского. Уже к октябрю 1893 года в него вошло 112 почетных членов, 55 из которых — из Европы и Америки. При этом выбить разрешение на международную подписку у властей было непросто. Комитет также реставрировал надгробие Лобачевского и учредил премию его имени для выдающихся ученых-геометров.
Торжественные телеграммы по случаю юбилея прислали различные научные организации, вузы и академии со всего света, а также знаменитые ученые, например Анри Пуанкаре и Дмитрий Менделеев. Была среди них и телеграмма от Петербургской академии наук. В ней академики признали свою ошибку в отношении Лобачевского. Празднование юбилея подхватили в других научных центрах страны, о Лобачевском писали в прессе, общей и научной.
Уже в советские годы удалось прояснить многие детали биографии Лобачевского. Так, историки Александр Андронов и Надежда Привалова выясняли дату и место рождения математика.
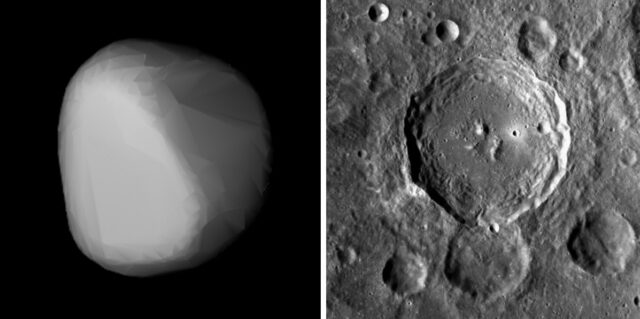
Ныне памятники Лобачевскому установлены в Казанском и Нижегородском университетах, на «Аллее ученых» в МГУ и в Институте электронной физики НАН Украины в Ужгороде. Имя первооткрывателя неевклидовой геометрии носят одна из малых планет (астероид) и кратер на обратной стороне Луны.
«Расставаясь с вами, что скажу вам поучительного? Вы счастливее меня, родившись позже. Из истории народов видели вы, что всякое государство переходит возрасты младенчества, возмужания и старости. То же будет и с нашим отечеством. Хранимое судьбою, медленно возвышается оно в своем величии и достигает высоты, на которую еще не восходило ни одно племя человеческое на земле. Век Петра, Екатерины, Александра были знамениты; но счастливейшие дни России еще впереди. Мы видели зарю, предвестницу их, на востоке; за нею показалось солнце... Я всё сказал этим».
Из речи Н.И. Лобачевского «О важнейших предметах воспитания»
