«Я на обед ем капусту, мой сосед ест котлеты, а в среднем мы с ним едим голубцы». Как понимать статистику

Многие уже поняли, что среднее арифметическое зарплат и его динамика не лучший способ анализа благосостояния граждан уездного города N, и начали требовать медианных значений. Это здравое желание, но, к сожалению, медиана тоже не всегда дает результат, нужный недовольным комментаторам. Как же перестать ненавидеть Росстат и зажравшихся энчан и полюбить статистику?

«Есть три вида лжи: маленькая ложь, большая ложь и статистика» (2-е место в хит-параде шуток про статистику).

Сами по себе данные не хорошие и не плохие. Вопрос только в том, что мы видим за этими числами. Чтобы лучше понимать, о чем нам хочет сказать очередной пресс-релиз комитета статистики уездного города N, нужно говорить со статистической наукой на одном языке. Конечно, среднее арифметическое — это далеко не все, а лишь одна из характеристик выборки. К сожалению, в школе вся математическая статистика сводится исключительно к нему. Возможно, именно потому, что жители N не знают других терминов, пресс-секретарь статистического ведомства публикует именно эту характеристику (нет, совсем не потому, что мэру нужно отчитаться).

Допустим, сегодня вышел пресс-релиз:

на центральной площади перед ратушей уездного города N провели выборочный опрос и выяснилось, что средний заработок энчан составляет 60 у. е. В паблике «Подслушано N» сразу начались словесные баталии. Появились комментарии о том, что ни у кого из знакомых автора зарплаты больше 30 у. е. нет, а такое значение возможно только потому, что статистическое ведомство лжет или у мэра зарплата в 10 000 у. е. Ну и обязательная шутка про голубцы, куда же без нее.

Кто же лжет в славном городе N: мэр, статистическое ведомство или же кто-то еще?

Чтобы разобраться, начнем с понятия выборки. Правильно сформировать выборку для опроса — особый квест. Очевидно, что если бы мы могли опросить всех горожан, то получили бы информацию о доходах всей популяции. Эта выборка точно была бы репрезентативной. Однако мы можем опросить не всех, а только некоторую часть жителей. И чем меньше людей участвует в опросе, тем ниже репрезентативность данных.

Можно ли считать выборку случайных людей на центральной площади репрезентативной? Однозначного ответа нет. На этот показатель может влиять день недели (будний/выходной), приезд делегации из столичного города M и еще очень много других факторов. В идеале после опроса все демографические соотношения (мужчины/женщины, дети/взрослые/пенсионеры и прочие) должны совпадать с общегородской статистикой — для этого и проводится перепись населения. Если выборка не отвечает этим требованиям, то она нерепрезентативна, а значит, это ошибка и доверять такому отчету нельзя.

Допустим, что выборка была репрезентативной, но данные для большинства горожан всё равно удивительные. Они таких зарплат даже не видят. Чтобы понять, почему среднее арифметическое позволяет довольно точно оценить знания школьников, посчитав средний балл за контрольную, не очень помогает оценить среднюю температуру по больнице и совершенно не работает при оценке доходов населения, нам понадобится понятие дисперсии.

Дисперсия — это мера «разброса» случайной величины от ее самого вероятного значения. У учеников оценка может быть от 2 до 5. Если мы считаем, что наиболее вероятная оценка у школьников 3,5, то мы имеем дисперсию, равную 1,5. Это небольшая дисперсия. Она позволяет нам говорить о том, что среднее арифметическое класса достаточно показательно, если мы хотим сравнить, какой класс знает математику лучше. При помощи такой аргументации гораздо проще объяснить маме тройку, чем доказывать, что у всех вообще два. Согласитесь, «Мама, я сделал вывод, что моя тройка с плюсом выше среднего арифметического в классе, что говорит о том, что я заслуживаю поощрения, а не наказания» звучит гораздо убедительнее, чем «Мама! Да у всех вообще двойки!».

В случае со средней температурой по больнице всё становится интереснее. Дисперсия температуры у живого человека не такая уж большая — от примерно +34 до +42 °С при максимально ожидаемой +36,6 °С. Это позволяет нам говорить, что среднее арифметическое достаточно показательно для оценки ситуации. Можно сказать, что в среднем пациенты в инфекционном отделении теплее пациентов в травматологическом. Однако всё меняется, если добавить труп с комнатной температурой. Это увеличивает дисперсию и приводит к тому, что среднее становится совершенно нерепрезентативным.

Точно так же можно посмотреть на статистику среднего возраста рождения первого/второго/третьего ребенка у женщины. Почему все учитывают именно женщин, а не мужчин? С агрегацией данных по мужчинам возникает много проблем: разная дисперсия по сравнению с женщинами (у женщин период, когда они могут иметь детей, гораздо короче, чем у мужчин), принципиально разное количество детей, которые могут появиться в течение жизни, сложности с достоверным установлением отцовства.

Несколько лет назад одна лаборатория опубликовала статистику, согласно которой около 10 % тестов на отцовство были отрицательными. Человек, который не знаком со статистикой, мог бы предположить, что 10 % детей воспитываются не своими родителями. Это одна из классических ловушек восприятия статистической информации, которая хорошо накладывается на предыдущие выводы по поводу однородности выборки:

«Никогда не переносите данные опроса на всю популяцию, если не убедились в корректности выборки».

В нашем случае отцовство действительно не подтвердилось в 10 % тестов, но что это была за выборка? Это люди, которые уже настолько сомневались в отцовстве, что пошли проверять его в лабораторию.

Перейдем к нашему вопросу с зарплатами. Дисперсия у зарплат может более чем в 10 раз превышать наиболее вероятный доход. Именно из-за этого говорить о среднем арифметическом как о репрезентативном показателе зарплаты гражданина из массы совершенно бессмысленно.

Понять, что происходит с зарплатами в городе N, помогут медиана и мода.

Медиана — это значение, при котором половина измерений будут больше нее, а половина — меньше нее.

Мода — самое часто встречающееся значение.

Посмотрим, что насчитал нам статистический орган города N. Пресс-секретарь утверждает, что распределение по полу, возрасту, месту жительства и виду деятельности совпадает с общегородским, то есть опрос репрезентативен.

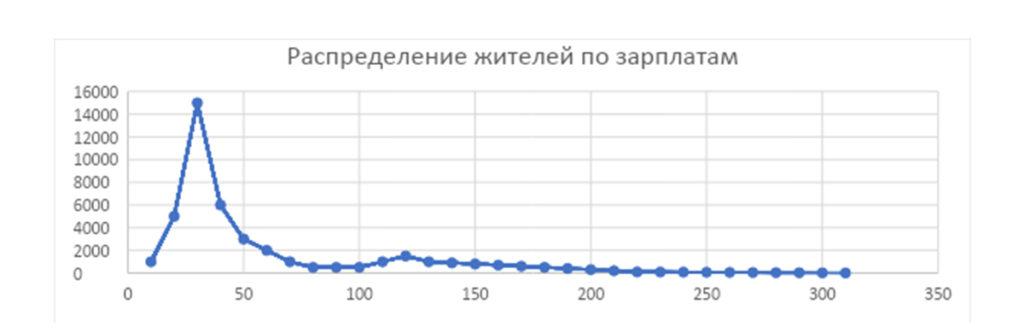
В нашем городе получились следующие показатели:

Средняя зарплата составила 60 у. е., однако такой зарплатой и выше могут похвастаться только 12 тысяч из 43 тысяч опрошенных, то есть около четверти населения N. Такое неравенство не может не вызывать удивления у жителей, и чем больше будет дисперсия по зарплатам в нашем городе, тем меньше энчане будут доверять значению средней зарплаты.

Посмотрим теперь на моду и медиану.

Медиана составит 40 у. е., а мода — 30 у. е. Мода — высокий пик на графике в 15 тысяч человек, примерно такого результата горожане и ожидают.

В моде практически каждый житель города узнает себя, своего знакомого или, по крайней мере, не удивится такому значению.

В нашем случае мода немного больше, но тоже не вызовет особого возмущения.

Каждая характеристика распределения позволяет что-то понять о распределении, однако даже все вместе они могут подводить. Например, модальное значение может быть совершенно случайным на малых выборках или если мы попробуем спрашивать о зарплате у людей с точностью до копейки. Тогда три человека с абсолютно одинаковой зарплатой могут иметь самое частое значение в выборке.

Другая ситуация — если у нас есть два равных пика. Например, в N не одно, а два градообразующих предприятия, причем одно из них в четыре раза успешнее другого. Мы получим вот такое распределение по зарплатам:

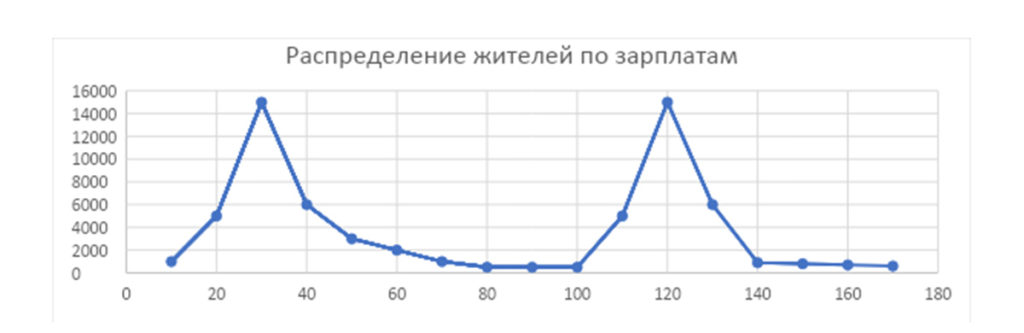
Здесь у нас получатся две моды: 30 и 120. Медиана будет 65, а средняя зарплата по городу будет 76. Полноценную картину может дать только общий набор данных.

Где и как мы можем применить эти знания в реальной жизни? Главным хранилищем «живых» данных в России является Госкомстат. Статистические показатели со всей страны собираются там и оседают на серверах ГКС. К сожалению, исходные данные по большинству вопросов не публикуют из соображений конфиденциальности, но что-то можно вытащить и оттуда. На gks.ru очень много разной статистики.

Кроме того, на сайтах ГСК, ВЦИОМа и прочих структур, которые связаны с оценкой и исследованием чего-либо в обществе, есть методологии, которым рассчитывается тот или иной показатель. Например, Франция при подсчете ВВП учитывает наличие собственного жилья у человека как его доход, что существенно повышает показатели.

Так что просто сравнивать ВВП, которые посчитаны по различным методологиям, тоже не лучшая затея.

C сайта ГКС можно скачать куб и базу данных. Пространство для игр с данными там просто безгранично.

Не стоит воспринимать контринтуитивную статистику как заведомый обман, но и доверять ей на все сто не надо. Статистика ради статистики — удел весьма своеобразных людей, вся остальная статистика собирается под конкретные запросы и задачи. Если же всплывают какие-нибудь данные, которые вызывают массовые бугурты, — возможно, эту информацию собирали не для общего пользования. Опять же, любые данные, которые вызвали у вас вопросы, можно проверить на адекватность, размер выборки и сохранение пропорций. Если отнестись к этому с чуть большим уважением и любопытством, можно открыть для себя огромный мир данных, из которых можно получать очень любопытные зависимости и последовательности.

Дерзайте знать.