Для чего нужна математика? Геометр Виктор Васильев — о своей науке, просветительской роли математиков и о том, как фальсифицируют исследования

Оглавление:

• Об образовании и просвещении
• О фальсификации науки
• О математике
• Об учениках, коллегах и математическом сообществе

Об образовании и просвещении

— Зачем нужна математика неспециалисту?

— Математика — это способ правильно рассуждать. Как говорил Фейнман, «математика — это не только язык науки, это — сконцентрированный опыт точного мышления множества людей».

— Однако среднее образование от этого идеала очень далеко. Обычный школьник, скорее всего, думает, что математика — это такая деятельность, где до бесконечности нужно что-то вычислять по заданным правилам. Всё, что связано с правильным рассуждением, уходит в кружки или становится прерогативой людей, которые по каким-то причинам этим заинтересовались.

— Наверное, так исторически сложилось, что люди не хотят думать.

Бесконечный источник задач — это тригонометрические уравнения, то есть дрянь, которую можно просто штамповать.

И те, кто не хотят думать, их штампуют, тем более что они есть в вузовских вступительных экзаменах.

В ЕГЭ по математике всё же что-то меняется. Кампания Ященко внесла хоть какое-то оживление в эту систему, но хороших учителей, которые понимают суть предмета, по-прежнему очень мало.

— Вы долго работали в комиссии РАН по экспертизе школьных учебников математики — можете назвать действительно хорошие?

— Учебники Башмакова и учебники под редакцией Шарыгина, Дорофеева, Бунимовича мне нравятся.

— А какую роль играют математики в просвещении общества?

— Есть положительный опыт. Например, Николай Андреев издает книгу «Математические этюды», да и всегда были хорошие книжки — та же «Что такое математика?» Р. Куранта и Г. Роббинса.

—  Эти книжки (тираж — 3 тысячи экземпляров) купят в основном самые заинтересованные школьники, часть из которых станет математиками, а часть — программистами. Но если мы говорим о коммуникации с широким сообществом людей в контексте важности методов точного рассуждения, отделения истинных суждений от ложных, то она не может касаться только книжек для заинтересованных школьников.

— На эту тему есть замечательная книга американца Джордана Элленберга «Как не ошибаться. Сила математического мышления», которую издал фонд «Эволюция». Она начинается с такого примера: командование американских ВВС поручило своим летчикам выяснить, на какую часть самолета нужно установить наиболее прочную броню. Они осмотрели вернувшиеся на базу самолеты, отметили, в каких частях находится большее число пробоин и сделали вывод: раз туда чаще всего попадают, надо дополнительно укрепить именно эти части. На что ученый-математик сказал: «Вы идиоты». Он не так сказал, конечно, но суть в том, что при обстреле пули попадают равномерно. Следует выяснить, где больше всего пробоин у самолетов, которые не вернулись, — эти части и надо укреплять. И это решение, вероятно, спасло тысячи самолетов и людей.

О фальсификации науки

— Вы — председатель комиссии по противодействию фальсификации научных исследований, чья деятельность широко освещалась в связи с выборами в РАН. В чем вы видите свою задачу?

— Это дело очень важное, которое нельзя не поддержать. Понятно, что стоит вкладываться, когда ты находишься близко к точке бифуркации и от тебя действительно что-то зависит. Проблема фальшивых диссертаций, статей, плагиата ужасна, и от нее опускаются руки. В какой-то момент мне стало казаться, что ничего с этим сделать нельзя, но когда появился «Диссернет», родилась надежда.

— В математике, на ваш взгляд, есть такая проблема? Если посмотреть на статистику, то там не очень много плагиата — «Диссернет» просто «не ловит»?

— В математике она не на таком уровне. «Диссернет» «вылавливает» большую часть, но только то, что на поверхности.

— Например, если чиновник заказал сделать работу и эту работу ему сделали плохо?

— Бывает по-разному. Резонансные случаи, когда ВАК упирается, начинается скандал, как раз такие: важный чиновник, серьезный совет. И есть большое количество случаев, когда ВАК с радостью соглашается c «Диссернетом»: мелкая сошка, коллега что-то списал. «Вы указали, а мы проявили принципиальность», — говорит ВАК.

Но надо развиваться. Может быть, с повышением околонаучной нравственности, репутационной ответственности оно как-то само собой будет изживаться.

— «Диссернет» реально что-то меняет в этой области?

— Ловят реальную сволочь, которая уже совершенно обнаглела. Если бы они знали, что их поймают, то стали бы это делать хитрее. Но они распустились и вляпались по полной программе. Их отловить и выставить на всеобщее обозрение — это великое дело, потому что больше они ничего выдумать не смогут.

— Эти не смогут, другие смогут: есть рынок заказных работ, просто люди будут делать это более качественно.

— И рынок есть, и люди будут, но сама демонстрация того, что с этим надо бороться, что это ненормально, для многих является положительным фактором.

О математике

— Что для вас математика и занятие математикой?

— Это такая деятельность, которой я по воле судьбы занялся. Оказалось, что я с ней справляюсь и она мне нравится — вот, собственно, и всё.

Всё начинается с задачи. Ты ее обдумываешь, появляются какие-то образы, начинаешь разбираться. Вопрос, который часто задают: математика — это строительство или кладоискательство? Для меня математика — это поиск источников, поиск подземной воды, которая была всегда. Я не строитель, я разбираюсь с тем, как оно есть на самом деле.

Я занимался довольно большим количеством задач, одна из них — задача по теории узлов: все знают, что есть задача и в ней я что-то придумал [речь идет об инвариантах Васильева-Гусарова). — Прим. CФ]. При этом образы были совсем из другой науки — теории особенностей; потом оказалось, что их можно применить к узлам, проинтерпретировав достаточно «потайным» образом. За одними картинками прячутся картинки совсем другого рода.

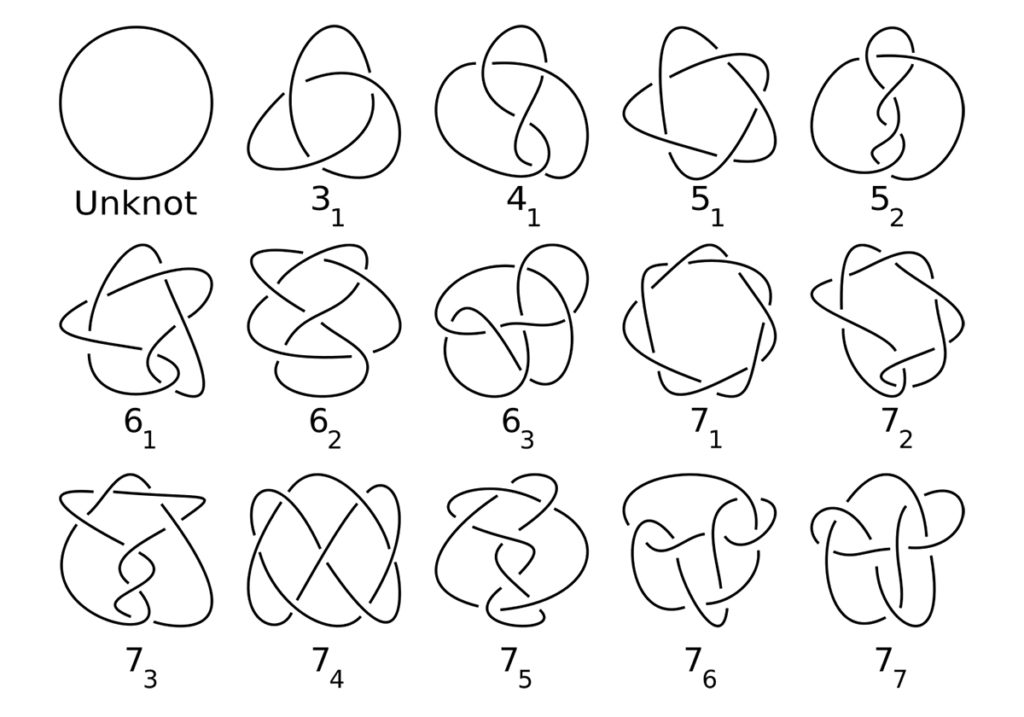
— Какая связь между теорией узлов и теорией особенностей?

— Теорию особенностей в популярных текстах еще называют теорией катастроф (хотя она и не сводится к последней). Это такая вещь: у нас есть множество всех объектов какого-то сорта. В этом множестве объектов есть объект, который чем-то выделяется. Если мы будем случайным образом рисовать кривую на плоскости, то почти все кривые будут выглядеть так, что у них есть только двукратные точки пересечения. А если мы рассматриваем все кривые, то в этом множестве есть кривые, в которых есть трехкратные точки пересечения или самокасания.

Интересно смотреть на эти выделенные объекты, потому что именно в них происходит перестройка из одной качественной ситуации в другую.

Например, можно посмотреть на пространство всех узлов — всех замкнутых кривых в трех измерениях. В этом пространстве лежат все узлы, все они связаны друг с другом. Это пространство — топологически тривиально, то есть две кривые можно соединить друг с другом. При этом они как-то перестраиваются. Полезно посмотреть на множество перестройки — множество кривых, которые отделяют узел одного типа от другого. А это — теория особенностей, и тут оказалось, что можно успешно применить некоторые трюки, которые я придумал раньше, для совсем других задач, в результате чего я попал в какую-то модную струю, это заметили.

— Работая с узлами, вы ожидали такого результата? Или же вы просто применили свой метод к модной задаче?

— Трюк, который я придумал, действительно решил какие-то известные задачи. Я был горд и очень радовался, когда мне это удалось сделать, но почему-то все обращали внимание только на решения задач, а сам мой метод, который мне так нравился, игнорировали. А мне очень хотелось, чтобы все заметили. И я стал искать какую-нибудь очень модную задачу, к которой его можно было бы применить, чтобы все поразились.

В это время была популярна теория узлов [речь идет о середине-конце 1980-х; в 1990 году Воган Джонс получил медаль Филдса за работы в этой области. — Прим. CФ], и я решил применить этот метод к ней. На самом деле основная цель не была достигнута, так как все сразу посмотрели, какие у меня ответы, и сумели это переформулировать в более элементарных терминах. Впрочем, кому надо, тот заметил: Максим Концевич и еще пара человек поняли, что за этим стоит.

— Но при этом идея всё равно осталась в форме трюка, она не превратилось в какую-то связную теорию?

— Нет, она превратилось, но об этом знает только узкая группа специалистов высокого уровня, не только Концевич, но еще несколько десятков людей. А картинки, связанные с узлами, понимают тысячи, но до них мои идеи так и не дошли. Этот метод применяется, в других областях с его помощью удается получить рекордные результаты, но это происходит во «взрослой» математике.

— А было ли наоборот: вы начинали с понятной задачи, и из нее рождался какой-нибудь интересный метод? Или же ваши мотивации всегда лежали в каких-то абстрактных областях?

— Исходные задачи очень часто были совершенно наглядные, а методы удавалось применять достаточно сложные.

Я на самом деле сейчас при всех общественных сложностях нахожусь в состоянии некоторой эйфории, потому что за последние 3 дня я добил задачу, которую пытался решить больше 30 лет.

Она не из самых знаменитых, но это был челлендж. Когда доказываешь гипотезу, очень радуешься. Придумать контрпример — это, как правило, немного похуже, но доказательство того, что он на самом деле эту гипотезу опровергает, — это тоже некоторая теория. Я уже в другом интервью Михаилу Сергеевичу Гельфанду для сборника «Математические прогулки» об этой задаче рассказывал.

Сама задача восходит к Архимеду и Ньютону, и у нее есть две ипостаси: четномерная и нечетномерная. Итак, пусть у нас будет какое-то тело в пространстве, например на плоскости, и мы рассматриваем множество всех гиперплоскостей в этом пространстве и на пространстве всех гиперплоскостей рассматриваем двузначную функцию — объемы двух частей, на которые гиперплоскость рассекает тело.

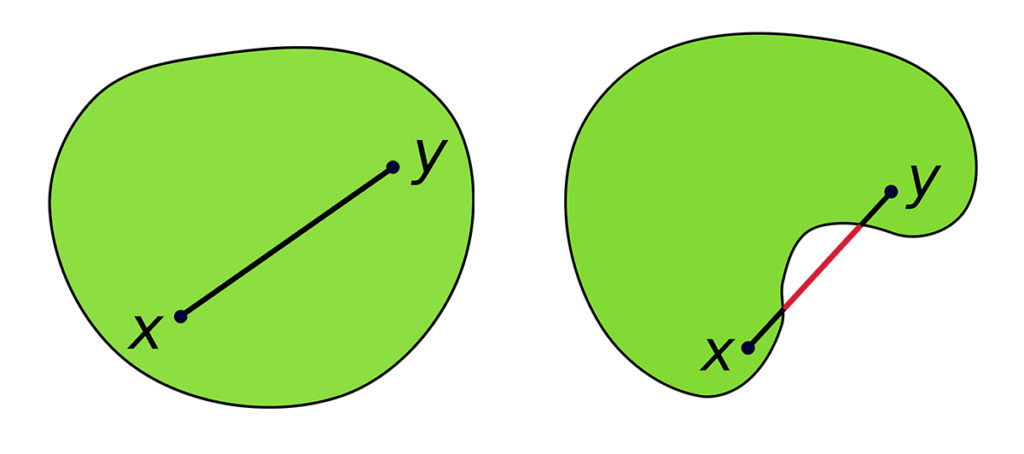
— Тело выпуклое (любой отрезок, имеющий концы внутри тела, сам лежит внутри тела)?

— Когда выпуклое — эта задача как раз менее сложная, ее решить достаточно быстро. Сложная задача — когда оно не выпуклое, любое тело, пусть — с гладкой границей. Вот такая функция. Вопрос в том, будет ли она алгебраической на пространстве всех гиперплоскостей?

Первая знаменитая теорема, которая принадлежит Архимеду говорит, что если это тело — шар в нашем пространстве, то да, это будет алгебраическая функция. А Ньютон доказал, что на плоскости таких тел не бывает, во всяком случае выпуклых.

Арнольд спросил: а как в других размерностях и как в невыпуклых случаях, и бывают ли другие примеры, кроме шаров? Я достаточно быстро тогда доказал, что для выпуклых тел в четномерном случае — не бывает, через двадцать с лишним лет доказал, что условие выпуклости тут не важно, и в четномерном случае задача полностью решилась.

И вот сейчас я придумал тело в нечетномерных пространствах, начиная с размерности 5, которое обладает такими же свойствами, что и шар.

— Оно связано с идеей Архимеда про шар или это что-то другое?

Тело достаточно простое: в пятимерном пространстве надо взять двумерную сферу, лежащую в трехмерном пространстве, и ее тоненькую трубчатую окрестность (трехмерный слой). Оказывается, это нетривиальный факт на самом деле, и функция будет алгебраической.

Вот такая геометрически наглядная картинка — она имеет вполне рекламный вид.

— Эта задача интересна сама по себе или у нее есть какие-то следствия в математике?

— В математике довольно много задач, которые сами по себе не имеют прямых применений. У теории узлов есть якобы какие-то приложения к теории струн. Такие задачи являются полигоном для отработки методов, и в этом главная ценность теории узлов. Теория наборов гиперплоскостей носит такой же характер. Данная задача тоже из этой серии. У меня есть книжка под названием «Ветвящиеся интегралы», в которой раскрывается интегральная геометрия и связанные с ней задачи математической физики.

Есть огромное количество функций в математической физике, имеющих такую же природу, как эта функция объема: в теории потенциала, в теории ударных волн; гипергеометрические функции, фейнмановский интеграл. Все это — интегральные функции. Там действуют похожие принципы, связанные с ветвлением интегралов, зависящих от параметров.

— А прикладными задачами вы занимались или, может быть, на вас повлияли какие-то нематематические идеи?

— Нематематические идеи на меня, пожалуй, не влияли. Некоторой прикладной тематикой я занимался, у меня даже был хоздоговор с текстильщиками из Университета де Монфорт в Лестере: это связано с теорией узлов, со способом плетения.

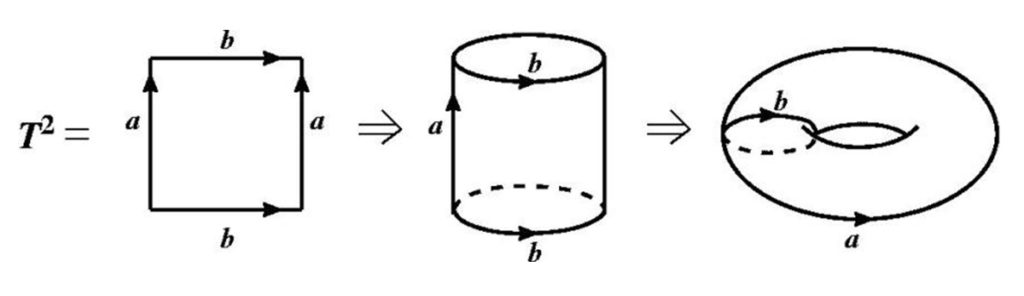
Ткань — это такой узел, состоящий из многих нитей, двоякопериодический; узор повторяется, его можно рассматривать как узор в клеточку, который продолжается на торе.

Теория узлов на торе ничем не хуже, а в чем-то и лучше, теории узлов в трехмерном пространстве. Вот, значит, классификацию какой-то системы автоматизированного проектирования этих самых текстильщиков из университета в Лестере я и делал. Из этого сотрудничества получилось пять сугубо математических статей. Потом они подавали заявки на какие-то гранты, но не выиграли.

Об учениках, коллегах и математическом сообществе

— Вы проработали всю жизнь в Москве — считаете ли вы при этом себя частью глобального математического сообщества? На ваш взгляд, советская математика находилась в изоляции?

— У меня опыт, надо сказать, непоказательный. Я никогда не чувствовал себя в изоляции, даже в советское время. Я ходил на семинары Гельфанда и Арнольда, последний притаскивал на них большие пачки журналов, которые получал как член редколлегии, и письма от своих зарубежных коллег.

Половина этих писем оседала в разных конторах, но половина доходила. Арнольд говорил: «Есть интересная задача — кто бы мог это сделать?» И старался ее кому-нибудь всучить. Иногда он прямо обращался к кому-то: «Вот вы, посмотрите, пожалуйста». И этих оттисков журналов и писем было больше, чем семинар мог переварить, от некоторых еще и отказывались. Из этих задач выросло довольно много всего.

— А вы сами общались с иностранными коллегами до перестройки?

— Почти нет. Лично я с ними не разговаривал. Несколько раз Арнольд давал какую-то задачу — я ее решал. Потом радостно писал письмо, скажем, Смейлу, что я, мол, познал вашу задачу. Через месяц получал от него ответ (или не получал, но от Смейла, слава богу, получил).

— То есть интенсивной переписки с коллегами из разных университетов не было?

— Это был совсем другой мир, тогда не было интернета. Чтобы послать письмо с непонятными закорючками, надо было его подписать в первом отделе. Конечно, это было очень трудно, и Арнольд делал великую вещь, что он эту часть коммуникации брал на себя, и весь наш семинар, как говорят религиозные люди, окормлял.

— Эта ситуация изменилась только в 1989 году?

— Ну да. В первый раз я оказался на Западе в 1990 году, на юбилее Смейла: он меня позвал, чтобы я рассказал о решении его задачи.

— Считаете ли вы, что есть какая-то «московская» математика, и насколько научные подходы в Москве могли отличаться от каких-то других, например во Франции или Америке, с точки зрения атмосферы или идей?

— Я не знаю. Опять-таки в молодости, когда я формировался, я был под большим влиянием Арнольда, мне были близки его взгляды и подход. Вот говорят — я не знаю, насколько это правда, — что в Америке не принято быть специалистом во многих областях, что они предпочитают изучать одну дисциплину, но глубоко. По мнению Арнольда, сила московской школы в том, что старались выучить всё, но я не стану этого утверждать. При том, что, безусловно, во Франции и в Америке есть универсалисты, такие как Делинь.

— А вы постоянно работали в Москве или на какие-то периоды выезжали?

— 3 раза я ездил на 3 месяца и 5 раз на месяц, бывал на международных конференциях.

— Ваши аспиранты в России работают или где-то еще?

— Два моих бывших аспиранта работают у нас на математическом факультете ВШЭ. Правда, один из них сильно изменил тематику, а другой, мой любимый ученик, работает в Канзасе. Вообще, учеников не так чтобы очень много. Остальные от меня ушли: кто-то — в программирование, кто-то — в другую науку.

— Вы не очень стремитесь брать аспирантов или вам сложно наладить контакт с ними?

— Может быть, я не очень хорошо оценивал их потенциал. Обычно я давал студенту, который ко мне просился, какую-нибудь задачу, которую я сам пытался решить, но она у меня не пошла. У некоторых получалось, но чаще выходило что-то бледное. Например, какую-нибудь курсовую или диплом написал, но дальше шел не ко мне.

— В России, даже в тех местах, где наука финансируется, математика все равно остается национальной. В МИАН, где мы сейчас находимся, работают ученые, которые родились в России, в крайнем случае ученые из Украины с российским гражданством. Вы бы хотели, чтобы научные институции стали более глобализированными, или же вы за сохранение национальных школ и локальных традиций?

— Хотелось бы, конечно, чтобы границы падали понемножку. Насколько это возможно — зависит не только от математики.

— Высшая школа экономики в какой-то период привлекла иностранных профессоров. Здесь, в МИАН, числились какие-то иностранные аспиранты, вроде бы из Нидерландов, но в целом это российское учреждение; Сколтех еще более интернационален, чем ВШЭ.

А вы предпочитаете заниматься математикой в окружении, которое говорит на русском языке, или когда всё обучение и семинары проходят на английском, иначе люди не поймут, о чем речь. Понятно, что есть разные варианты, но что, на ваш взгляд, лучше — работать всю жизнь в одном месте или перемещаться?

— Если смотреть статистически, то, конечно, больше добиваются успеха те, кто ездят: вот человек поучился здесь, узнал какой-то новый философский подход, съездил в другое место и там чему-то научился — это благотворно влияет на человека, хотя бывают исключения и люди бывают очень своеобразные. Вот Перельман очень своеобразный, хотя и он покатался.

Смена нескольких парадигм cкорее полезна. У меня тоже был такой опыт. Я долго учился у Арнольда, потом работал с Гельфандом, а это совсем другой подход. Было очень трудно перестраиваться, но это было очень важно.

Самые сильные люди получаются из тех, кто вобрал в себя знания из трех-четырех источников: натурфизического — у Арнольда и Гельфанда и алгебраической геометрии — у Шафаревича и Манина.

Концевич — тому пример, и это идеальный букет.

— Чем различались подходы Арнольда и Гельфанда?

Во-первых, они были разные люди, и, соответственно, на их занятиях эмоциональная обстановка была тоже разная. У Арнольда новое решение задачи было всегда связано с «выбросом» вдохновения, волшебства.

А у Гельфанда был подход совершенно профессиональный.

Он говорил: «В этом надо разобраться». Если человек не желал этого делать, Гельфанд закипал: «Что такое?! Если вы считаете себя профессионалом, что значит, что вы не знаете этой области? Если того требуют условиям задачи, то вы сядьте и выучите, иначе вы не профессионал, а…»

Он не совсем так формулировал, но смысл был ровно такой. Любимая была у Гельфанда поговорка — «кто в лавке остался»: всеми побочными вещами можно заниматься, но главное, чтобы дело двигалось. Арнольд производил более блестящее впечатление, а у Гельфанда была такая трудовая атмосфера: если ты работник, то ты уж работай.