Множество множеств: насколько велика бесконечность?

В конце блокбастера «Мстители: Финал» голограмма Тони Старка прощается со своей маленькой дочерью и говорит: «Я люблю тебя на три тысячи». Этот трогательный момент перекликается с другой сценой, где Старк с дочерью пытаются в игровой форме выяснить величину их любви друг к другу. По словам Роберта Дауни-младшего, играющего Тони Старка, эта сцена была вдохновлена разговорами с его собственными детьми.

Игра может стать увлекательным способом изучения больших чисел:

— Я люблю тебя на десять из десяти.
— Но я люблю тебя на все сто.
— А я тебя на сто один!

Именно так слово «гуголплекс» стало популярным в моем доме. Но всем известно, к чему в конечном счете приводит этот спор:

— Я люблю тебя бесконечно!
— О, в самом деле? А я люблю тебя бесконечно плюс один!

Таким образом дети сталкиваются с понятием бесконечности задолго до уроков математики — на игровой площадке или перед сном, и неудивительно, что это таинственное и сложное понятие их так увлекает. Некоторые из этих детей вырастают математиками, очарованными бесконечностью, а некоторые из этих математиков открывают ее новые удивительные свойства.

Возможно, вы знаете, что ряды чисел могут быть бесконечно велики, но знаете ли вы, что некоторые бесконечности больше других?

Математики размышляли над этим вопросом по меньшей мере столетие, и некоторые недавние работы внесли в него некоторую ясность.

Чтобы ответить на вопросы о размере бесконечных множеств, давайте начнем с множеств, которые всё же поддаются счету. Множество — это набор объектов или элементов, а конечное множество — это множество, содержащее конечное число объектов.

Определить размер конечного множества несложно: просто подсчитайте количество элементов, которые оно содержит. Поскольку ряд конечен, вы знаете, что в конце концов перестанете считать, и когда вы закончите, вы узнаете размер этого ряда.

Эта стратегия не работает с бесконечными рядами. Вот набор натуральных чисел, обозначенный ℕ. (Некоторые могут возразить, что ноль не является натуральным числом, но этот спор не влияет на наше исследование бесконечности.)

ℕ={0,1,2,3,4,5,…}

Каков размер этого ряда? Поскольку самого большого натурального числа не существует, подсчитать количество элементов не получится. Конечно, можно объявить размер этого бесконечного множества равным «бесконечности», и это не будет ошибкой, но если требуется изучить и другие бесконечные множества, становится понятно, что такой подход тоже не совсем продуктивен.

Рассмотрим набор действительных чисел, которые представляют собой все числа, выражаемые в десятичном разложении, например 7; 3,2; −8,015, или в бесконечном представлении, например 2‾√ = 1,414213 …. Поскольку каждое натуральное число также является действительным числом, множество действительных чисел настолько же большое, как и множество натуральных чисел, поэтому оно тоже должно быть бесконечным.

Однако если мы объявими, что ряд действительных чисел настолько же «бесконечен», как и ряд натуральных чисел, мы столкнемся с кое-какой проблемой. Чтобы понять, какой, выберите любые два числа, например 3 и 7. Между этими двумя числами всегда будет конечное число натуральных чисел: здесь это числа 4, 5 и 6. Но между ними всегда будет бесконечно много действительных чисел, таких как 3,001; 3,01; π; 4,01023; 5,666… и т. д.

Примечательно, что, независимо от того, насколько близки друг к другу два любых действительных числа, между ними всегда будет бесконечно много действительных чисел.

Само по себе это не означает, что множества действительных чисел и натуральных чисел имеют разные размеры, но вместе с тем важно понимать, что между двумя этими бесконечными множествами есть несколько принципиальных отличий, которые требуют дальнейшего изучения.

Математик Георг Кантор исследовал их в конце XIX века. Он показал, что два этих бесконечных множества действительно имеют разные размеры. Чтобы понять и оценить, как ему это удалось, сначала мы должны понять, как сравнивать бесконечные множества. Секрет прост: функции.

Существует множество различных способов думать о функциях — запись функций, вроде f(x)=x2+1, графики парабол в декартовой плоскости, такие правила, как «возьмите входные данные и добавьте к ним 3» — но мы будем думать о функции как о способе сопоставления элементов одного числового ряда с элементами другого.

Давайте примем множество натуральных чисел за ℕ. Для другого ряда, который мы назовем S, мы возьмем все четные натуральные числа. Вот два этих ряда:

ℕ={0,1,2,3,4,…} S={0,2,4,6,8,…}

Существует простая функция, которая превращает элементы ℕ в элементы S. Вот она f(x)=2x. Эта функция просто удваивает свои входные данные. Мы получим такой ряд: f(0)=0, f(1)=2, f(2)=4, f(3)=6 и т. д.

Вы можете визуализировать это, выстроив элементы двух рядов друг напротив друга и указав стрелками, как функция f преобразует входные данные из ℕ в выходные данные в S.

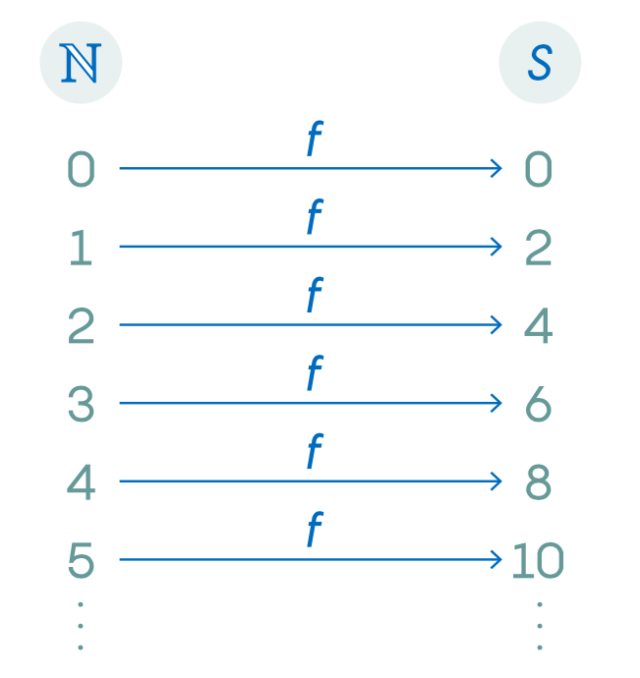
Обратите внимание, как f(x) присваивает ровно один элемент ряда S каждому элементу ряда ℕ. Это то, что делают функции, но f(x) делает это особым образом. Во-первых, f присваивает всё в элементы S каким-нибудь элементам в ℕ. Используя функциональную терминологию, мы говорим, что каждый элемент S является «образцом» элемента ℕ в функции f. Например, четное число 3472 находится в S, и таким образом мы можем вычислить x в ℕ: если f(x) =3472, то это 1736. В таком случае мы говорим, что функция f(x) отображает ℕ на S. Более причудливый способ сказать это состоит в том, что функция f(x) является «сюръективной». Так или иначе, здесь важно вот что: поскольку функция f(x) превращает входные данные из ℕ в выходные данные в S, никакие элементы в S не пропадают в процессе.

Вторая особенность того, как f(x) присваивает выходные данные другому ряду, заключается в том, что никакие два элемента в ℕ не преобразуются в один и тот же элемент в S. Если два числа разные, то их удвоения различны; 5 и 11 — разные натуральные числа в ℕ, и их выходные данные в S также различны: 10 и 22. В этом случае мы говорим, что f(x) равняется «1 к 1» (также пишется «1–1»), и мы описываем f(x) как «инъективную» функцию.

Ключевой момент здесь в том, что каждый элемент в S сопряжен только с одним элементом в ℕ.

Эти две особенности f(x) сочетаются любопытным образом. Функция f(x) создает идеальное соответствие между элементами ℕ и элементами S. Тот факт, что f(x) является функцией «отображения», означает, что у всех элементов в S есть партнер в ℕ, а тот факт, что f(x) равно 1 к 1, означает, что ни у какого из элементов в S нет двух партнеров в ℕ. Короче говоря, функция f(x) связывает каждый элемент ℕ ровно с одним элементом S.

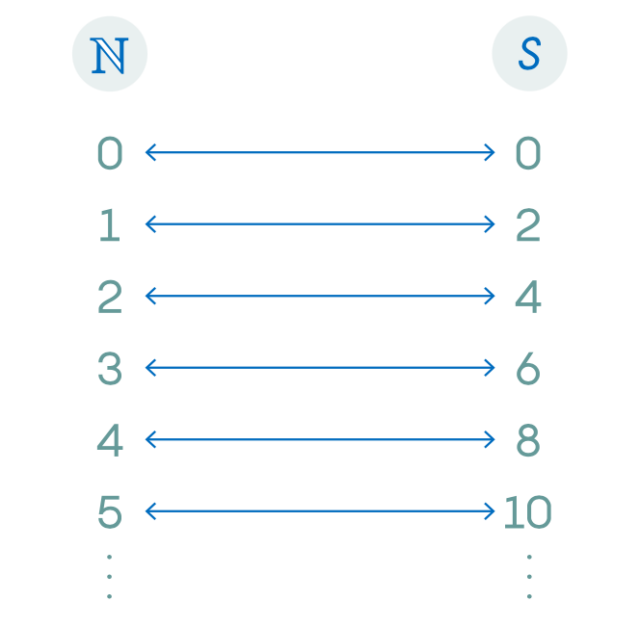
Функция, которая является одновременно инъективной и сюръективной, называется биекцией, и биекция создает соответствие 1 к 1 между двумя рядами. Это означает, что каждому элементу в одном ряду соответствует ровно один элемент в другом ряду, и это один из способов показать, что два бесконечных ряда имеют одинаковый размер.

Поскольку наша функция f(x) является биекцией, это значит, что два бесконечных множества ℕ и S имеют одинаковый размер. Это может показаться удивительным: в конце концов, каждое четное натуральное число само по себе является натуральным числом, поэтому ℕ уже содержит все элементы S и даже больше. Разве это не должно сделать ℕ больше, чем S? Если бы мы имели дело с конечными множествами, ответ был бы утвердительным. Но один бесконечный ряд может полностью содержать другой, и они всё равно могут быть одного размера, наподобие того, как «бесконечность плюс один» на самом деле не является большим количеством любви, чем «бесконечность» сама по себе. Это лишь одно из многих удивительных свойств бесконечных множеств.

Еще большим сюрпризом может стать то, что существует бесконечное множество рядов разных размеров. Ранее мы исследовали различную природу бесконечных множеств действительных и натуральных чисел, и Кантор доказал, что эти два бесконечных множества имеют разные размеры. Он сделал это с помощью своего знаменитого диагонального аргумента.

Поскольку существует бесконечно много действительных чисел между любыми двумя различными натуральными числами, давайте просто сосредоточимся на бесконечно многих действительных числах между 0 и 1. Каждое из этих чисел можно рассматривать как (возможно, бесконечное) десятичное разложение, подобное этому:

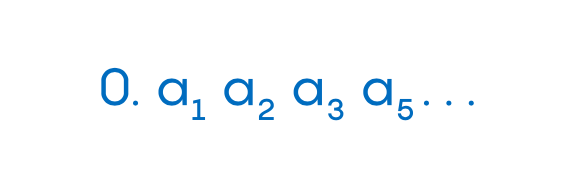
Здесь a₁, a₂, a₃ и т. д. — это просто порядковый номер числа, но нам нужно, чтобы не все цифры были равны нулю, поэтому мы не включаем само число ноль в наш ряд.

Диагональный аргумент, по сути, начинается с вопроса: что произошло бы, если бы между натуральными числами и этими действительными числами существовала биекция? Если бы такая функция действительно существовала, два набора имели бы одинаковый размер, и вы могли бы использовать функцию для сопоставления каждого действительного числа от нуля до 1 с натуральным числом. Вы могли бы изобразить упорядоченный перечень соответствий, например, таким образом:

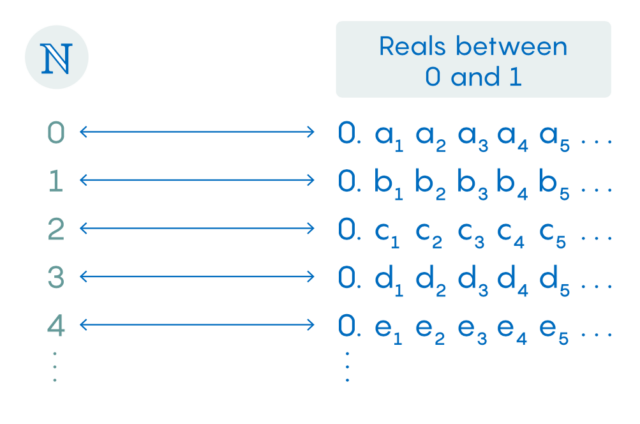
Гениальность диагонального аргумента заключается в том, что вы можете использовать этот перечень для построения действительного числа, которого в нем не может быть.

Начните строить действительное число цифра за цифрой следующим образом: сделайте первую цифру после десятичной точки чем-то отличным от a₁, сделайте вторую цифру чем-то отличным от b₂, сделайте третью цифру чем-то отличным от c₃ и т. д.

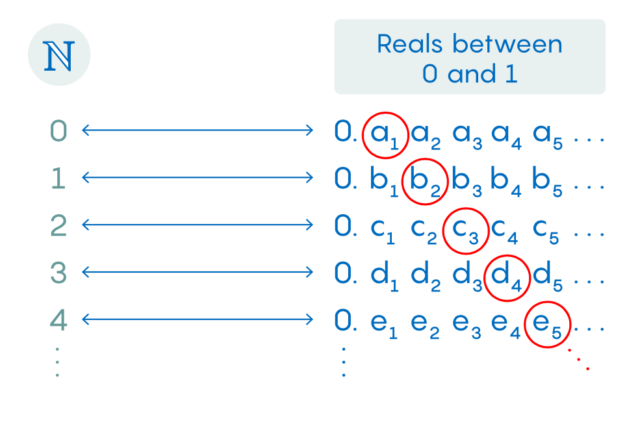
Это действительное число определяется его отношением к числу, расположенному на диагональном перечне. Есть ли оно само в этом перечне? Оно не может быть первым числом в перечне, так как у него другая первая цифра. Оно также не может быть вторым числом в перечне, так как у него другая вторая цифра. Фактически оно не может быть n-м номером в этом перечне, поскольку у него другая n-я цифра. И это верно для всех n, поэтому это новое число, которое находится между 0 и 1, но не может находится в перечне.

Но в нем должны были быть все действительные числа от 0 до 1! Это противоречие возникает из предположения, что существует биекция между натуральными и действительными числами между 0 и 1, и поэтому такая биекция не может существовать. Это означает, что эти бесконечные множества имеют разные размеры. Еще немного поработав с функциями, можно показать, что множество всех действительных чисел имеет тот же размер, что и множество всех действительных чисел от 0 до 1, и поэтому действительные числа, которые содержат натуральные числа, должны быть бóльшим бесконечным множеством.

Техническим термином для обозначения размера бесконечного множества является мощность. Диагональный аргумент показывает, что мощность действительных чисел больше, чем мощность натуральных чисел. Мощность натуральных чисел записывается ℵ0 (произносится как «алеф ноль»). В стандартном представлении математики это наименьший бесконечный кардинал.

Следующий бесконечный кардинал равен ℵ1 («алеф один»), и математиков уже более столетия ставит в тупик простой вопрос: является ли ℵ1 мощностью действительных чисел? Другими словами, существуют ли какие-либо другие бесконечности между натуральными числами и действительными числами? Кантор думал, что ответ будет отрицательным — утверждение, которое стало известно как гипотеза континуума, — но не смог это доказать. В начале 1900-х годов этот вопрос считался настолько важным, что, когда Дэвид Гильберт составил свой знаменитый список из 23 важнейших нерешенных задач математики, гипотеза континуума была в нем под номером 1.

Сто лет спустя был достигнут значительный прогресс, но он привел к новым загадкам. В 1940 году знаменитый логик Курт Гедель доказал, что в соответствии с общепринятыми правилами теории множеств невозможно доказать, что существует бесконечность между натуральными и действительными числами. Это может показаться большим шагом к доказательству того, что гипотеза континуума верна, но два десятилетия спустя математик Пол Коэн доказал, что также невозможно доказать, что такой бесконечности не существует!

Оказывается, гипотеза континуума не может быть доказана тем или иным способом.

В совокупности эти результаты доказали «независимость» гипотезы континуума. Это означает, что общепринятые правила относительно множеств просто не могут сказать нам, существует ли бесконечность между натуральными числами и действительными числами. Однако математики не обескуражены этим фактом — они приняли вызов. Сейчас они ищут новые фундаментальные правила для бесконечных множеств, которые смогут и объяснить то, что уже известно о бесконечности, и помочь заполнить существующие пробелы.

Говорить «Моя любовь к тебе не зависит от аксиом», возможно, не так весело, как говорить «Я люблю тебя бесконечно плюс один», но, возможно, это поможет следующему поколению математиков, любящих бесконечность, хорошо выспаться ночью.