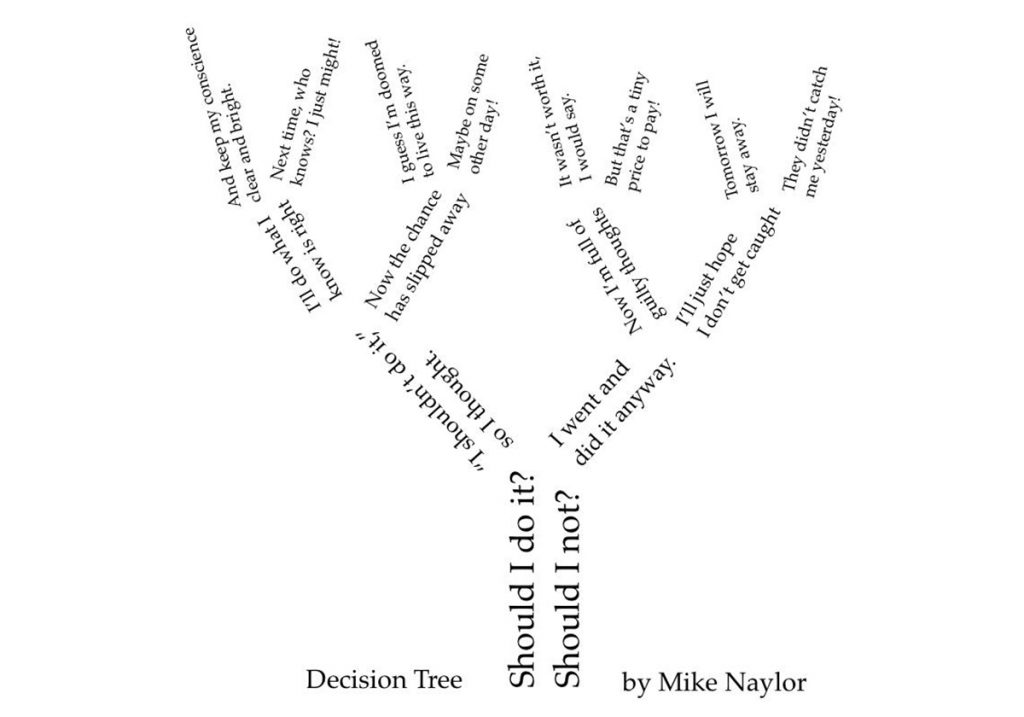
— Ваше первое образование было физико-математическим. Можно ли говорить об особом складе ума, который требуется для занятий техническими науками? И насколько он совместим с занятиями литературой и литературоведением? Не ограничивает ли он его?
— Мое первое образование — естественно-научное, физико-техническое, но склонность у меня была всегда больше к математике. Это разные «склоны» ума: математика действует в идеальном мире идеальных объектов и законов, где постулаты определяют аксиомы, из аксиом выводятся теоремы, исходя из доказанных теорем решаются задачи... До того предела, когда заключения теорем начинают друг другу противоречить, я не доходила, хотя умозрительно понимаю эту неизбежность. Я скорее различала начальные постулаты и далее начальные условия, которые могут привести к бесконечному расхождению результатов. И всё же все траектории будут описываться тремя простыми формулами. Это математика.

В физике иначе: там погрешности, ошибки измерения, точность приборов, повторяемость результата, недостаточность данных, недостаточность средств для проведения эксперимента... Иной подход, и хотя я его и освоила в какой-то мере, мне была всегда ближе красота математики, в крайнем случае заоблачное великолепие теоретической физики.
Математический склад ума воспитывается, как мне представляется, любовью к решению задач, множества задач, везде, где найдутся, олимпиадных, занимательных, повышенной сложности, в журнале «Квант», в сборниках занимательных головоломок...
Это интересно: увидеть суть, найти решение, испытать эту мгновенную ясность — эта загадка решается только так и никак иначе!
Если это специальный склад ума, отличный от других, то литература ведь тоже бывает разная, требующая различных подходов к чтению. Мне близка умная, как сейчас называют, эргодическая литература, в которой как раз требуется искать решения, доискиваться сути. Как писали в эпоху барокко, «письмо с ключами», да и сейчас, нетривиальное письмо, не поверхностное. Мне кажется, занятия математикой помогают при чтении такой литературы. А уж когда приходишь к некоему пониманию сложно устроенного текста, затраченные усилия призывают к написанию статьи — из этого выросли мои литературоведческие экзерсисы о Жорже Переке, Флэнне О’Брайене и других. Так что в литературоведении это скорее помогает.
В каком-то смысле можно сказать, что математический склад ума ограничивает спектр чтения: какие-то книги, с зияющими пробелами в логике, например, я читать не могу. Зато от умных текстов получаю двойное наслаждение — и эмоциональное, и интеллектуальное.
— Как вы пришли к исследованию комбинаторной литературы и, в частности, творчества одного из основателей «Улипо» Раймона Кено?
— В 1999–2001 годах я училась во Французском университетском колледже при МГУ и Сорбонне. Занятия по литературе у нас вела Екатерина Евгеньевна Дмитриева. Она во многом на меня повлияла, многому научила и многое открыла. В какой-то момент, когда я уже искала тему для дипломной работы, я наткнулась на «Улипо» и Раймона Кено, сначала на «Голубые цветочки», а затем и на «Сто тысяч миллиардов стихотворений». Я пришла в совершенный восторг от этих работ, именно потому, что они снимали давнюю проблему выбора: заниматься литературой или точными науками.
Кено и «Улипо» продемонстрировали, как не отказываться от того или другого, но как одно может обогащать другое — в их случае, как и в моем, математика может обогащать литературу.
И когда я поделилась восторгом с Екатериной Евгеньевной, она предложила мне написать дипломную работу по «Ста тысячам миллиардов стихотворений». Из этой дипломной работы произросла моя диссертация, защищенная в 2003 году в РГГУ под руководством профессора Юрия Борисовича Орлицкого, и монография, изданная в 2006 году издательством «Бахрах-М», и многие статьи. Во многом это определило мою жизнь на следующие годы. И в начале пути была чудесная Екатерина Евгеньевна, человек, которого мне посчастливилось называть учителем.
— Каковы были предпосылки для создания «Улипо» и были ли или могли бы появиться подобные объединения в других странах?
— «Улипо» возникло в 1960 году, в эпоху, когда возникали идеи хиппи и рок-н-ролла, на заре возникновения массовых движений — студенческого, антивоенного. Это была эпоха праздника и благоденствия, но и начало нового противостояния — холодной войны и гонки вооружений. «Улипо» было создано поколением, которое в детстве пережило великую войну, а потом обрело мир и благополучие. Это была новая эпоха, а новая эпоха ищет и новые способы говорить о себе.
Незадолго до того во Франции возник «новый роман» с его «смертью автора» и «смертью персонажа». Цвела новая философия, самым популярным был, вероятно, Сартр, но и Батай, и Лакан... Поиски продолжались. Еще до войны во Франции возникала новая математика: если «новый роман» отказывался от Бальзака, то Бурбаки отказывались от Пуанкаре и вводили строгую аксиоматичность всей литературы. Возникло визуальное искусство, граничащее с математикой, — поп-арт.
И на пересечении этих поисков, новой философии, новой литературы, новой математики появляется уникальная фигура Раймона Кено, который слушал лекции Александра Кожева, который учился математике, который уже давно работал в издательстве «Галлимар», уже написал «Зази в метро», уже являлся Трансцендентным Сатрапом Патафизического коллежа. Отцом «Улипо» стал литератор, всерьез увлекающийся математикой. Предпосылками были свобода, страсть к познанию, к изучению сути, исследованию новых путей, новых (они же самые старые) способов написания текстов, к занимательным играм ума, играм языка...
Возможно ли было объединение типа «Улипо» в ином месте и в иное время — думаю, вполне. Но по ряду причин не сложилось. В иное время — было, взять хотя бы «Великих риториков» эпохи Позднего Средневековья. Хоть они и не собирались каждый месяц в замке выпить вина и обсудить свои труды, как Бурбаки, и не были группой в современном понимании, но представления о творчестве, мне кажется, у них были близки «Улипо».
В более позднее время, на микроуровне, такие группы тоже были. Легко могу себе представить группу советских физиков, пишущих стихи с естественно-научным уклоном. Но у нас было это противопоставление — физиков и лириков, и физики, талантливые в гуманитарных областях, уходили в эстраду, театр, кино, КВН (Александр Филиппенко, Вадим Абдрашитов, Юрий Морозов, Максим Пинскер), то есть в области лицедейства. Или не уходили из физиков, а литературой занимались в «свободное время», как, например, Геннадий Копылов.
Те же, кто шел в писатели, старались, чтобы их не заподозрили в подозрительном физико-техническом прошлом.
В студенческих театрах, газетах, клубах, КВНах естественно-научных вузов бродили те же дрожжи занимательной математики в применении к литературному, песенному, визуальному творчеству, но к сожалению, они не дозрели до всепланетного уровня «Улипо».
«Улипо» провели энциклопедическую, как принято у французов, работу по выявлению образцов «комбинаторного» творчества прошлого, системно исследовали всевозможные «ограничения» языка. И были чрезвычайно талантливы: Итало Кальвино, Жорж Перек, Жак Рубо... Видимо, от других групп, увлекающихся экспериментами, «Улипо» отличалась созвездием талантов, ко времени объединения уже профессионально работавших в литературе и математике и после образования группы посвятивших себя развитию новой литературы ограничений.
— Отличаются ли принципы и особенности комбинаторной литературы в разных национальных литературах?
— В России больше внимания уделяется буквенной комбинаторике: буквенным палиндромам в первую очередь, далее — анаграммам, есть немного слоговых упражнений, тоже в первую очередь анаграмм и палиндромов. Круговые палиндромы и визуальные комбинаторные формы уже проходят как экзотика, а перестановки строк и фраз уникальны.
Спектр «Улипо» много шире — от перестановок крупных текстовых фрагментов до иных формальных ограничений, как то: игры с последовательным чтением элементов текста, текстовыми конструкторами, экспериментами с рифмой и строфикой, возвращающих читателя во времена Средневековья, пробующего рифму на вкус.
Английская комбинаторика традиционно тяготеет к поэзии абсурда, чрезвычайно там распространенной. Исторически в Британии был абсурд, и все игры со словами волей-неволей примыкали к нему. Во Франции была тенденция научности и энциклопедичности, и литература ограничений примкнула к ней.
В России литература с элементами языковой игры лежала вне основных поэтических направлений, хоть большого официального советского стиля, хоть неофициального. Комбинаторика была «ненастоящей литературой», и ей редко когда удавалось выйти за рамки капустников и КВНа.
Еще можно назвать детскую литературу, по определению игровую и во многом комбинаторную (от Хармса до Сапгира), письмо «в стол» (Ладыгин, Хромов, Гершуни), филологические опыты (А. Кондратьев).
Еще одна особенность российской комбинаторной поэзии, во всяком случае, до последнего времени — это переоткрытие форм и приемов. Традиция была повсеместно неизвестна: не знали ни о М. Довгалевском, ни о С. Полоцком, ни о В. Хлебникове, ни о поэтах ХХ века, поскольку они писали в стол или печатались в близком самиздате. Так что новые авторы приходили в восторг, открывая «я ем змея», «муза разум», «город дорог» — это малые радости комбинаторики. Новые палиндромисты повторяли открытия прежних, лежащие в языке так же, как малые леммы лежат в математике.
— Есть ли у комбинаторной литературы и литературы ограничений какие-либо преимущества перед более привычными принципами создания литературных текстов?
— Давайте начнем с того, что всякая литература есть литература ограничений. Говорим мы о метре и рифме — это ограничение; говорим, что рифма может быть мужской и женской и они должны чередоваться, — это ограничение; говорим, что в верлибре не должно быть метра и рифмы, — и это ограничение; что в прозаическом тексте должна быть завязка, кульминация и развязка, — это ограничение; что предложение должно начинаться с большой буквы и заканчиваться одним из определенного набора знаков препинания, — тоже ограничение, и так далее и тому подобное.

Вопрос в том, воспринимается ли данное ограничение как общепринятое или же как маргинальное, искусственно созданное и примененное к тексту. Я не готова относить все комбинаторные формы и формулы ограничений к маргинальным методам. Здесь нужно уточнить, какие именно приемы вы имеете в виду. И понимать условность самого этого деления: вот эти формы мы будем считать комбинаторными приемами и формальными ограничениями и будем рассматривать их отдельно от других, не менее «ограниченных», но укоренившихся в литературной традиции и не воспринимающихся в отрыве от нее.
— Ваша диссертация, а потом и книга о «Ста тысячах миллиардов стихотворений» Раймона Кено — одно из самых известных исследований комбинаторной литературы на русском языке. Она, безусловно, обязательна к прочтению. А какие бы еще статьи или монографии вы выделили или посоветовали тем, кто решит продолжить изучение комбинаторной литературы (на всех языках)?
— 1. Материалы «Улипо», в первую очередь, классические:
- L’OULIPO: La littérature potentielle (Paris: Gallimard, 1973),
- Oulipo. Atlas de littérature potentielle (Paris, Gallimard, 1981),
- Anthologie de l’Oulipo (Paris, Gallimard, 2009).
2) Интересный диск по произведениям «Улипо»:
A. Denize and B. Magné. Machines à Ecrire, CD-ROM. Paris, Gallimard, 1999.
3) Сайт «Улипо».
4) Работы Мартина Гарднера, он писал о занимательной математике, в том числе и о литературных играх.
5) Русские тексты начала ХХ века разбирал М. Л. Гаспаров: Русские стихи 1890–1925 годов в комментариях (Москва, Высшая школа, 1993).
6) Современные антологии:
- Антология русского палиндрома, комбинаторной и рукописной поэзии (Москва, Гелиос АРВ, 2002),
- Свобода ограничения: антология современных текстов, основанных на жестких формальных ограничениях. Сост. Т. Бонч-Осмоловская, В. Кислов (Москва, НЛО, 2014).
7) Занятный блог о поэзии с математикой Джоан Гроуни.
В последнее время развиваются интернет-коллективные тексты, где люди участвуют в написании истории, разветвлений, новых сюжетов, разных финалов и историй без финалов. Я когда-то это подробно смотрела, но сейчас у меня ссылок нет, да и вообще это далекое будущее нашей комбинаторики.
Тексты завтрашнего дня — это интерактивные тексты, кибертексты, гипертексты, некоторые электронные тексты и так далее. Но это уже совсем другая история.
— Существуют ли, на ваш взгляд, иные способы включить математические операции и принципы в литературные тексты, кроме концептуализации формальных ограничений?
— Порядок и степень включения математики в литературу зависит от представлений автора о математике и литературе.
Действительно, прямые включения — это разнообразные формальные ограничения, когда размышления над математическим понятием приводят к его отражению в структуре текста. Например, последовательность чисел становится последовательностью слов с определенным числом знаков. Так получаются Пи-стихотворения, Фибоначчи-стихотворения, стихотворения на треугольнике Паскаля и так далее. Или неарифметические, негеометрические формы: фигурные стихотворения — по сторонам квадрата, по определенной кривой, по спирали, по многограннику, по лабиринту...
Другие методы — математика ведь шире, чем арифметика, планиметрия и теория групп, — есть логика, есть топология.
Текст может вырасти из математического понятия, обрастая вокруг него сюжетом и стилем, как дерево вырастает вокруг семечка.
Но внутри, в основе будет простая математическая конструкция. В детективах протагонист перебирает возможности, отбрасывая ложные, чтобы найти истину, — это логика, это математика. Когда герои Борхеса в рассказе «Смерть и буссоль» чертят ромб — это математика. Можно идти дальше, ко всем текстам, основанным на некоторой схеме — на картах Таро, шахматном поле, Древе Сефирот, схеме шифрования... Здесь не точное формальное ограничение, но структура, концептуально определяющая текст. Насколько жестко определяет, зависит от автора.

Логика, от классической до нелинейной, может увести автора куда угодно далеко — скажем, роман Дж. Хеллера «Уловка 22». Энтропия — понятие, описываемое математическим способом, и об энтропии размышлял Пинчон в одноименном рассказе. Еще одно размышление об энтропии — рассказ Айзека Азимова «Последний вопрос». Существует ряд завораживающих математических понятий, о которых размышляют писатели, поэты, даже музыканты, далеко уходя от исходного понятия к человеку и человечности. Аналогично с ядерной физикой — ничто не мешает Нику Кейву размышлять о бозоне Хиггса!
Совсем другой способ — занимательные образовательные истории. Существует целый ряд таких текстов, в которых рассказывается о математических понятиях и задачках. Это серия текстов Э. Эдвина «Флатландия» — рассказы о вымышленной стране, обитатели которой плоские. «История с узелками» Льюиса Кэрролла — джентльмены путешествуют, дамы собирают на стол, попутно встречая и загадывая разнообразные загадки. Заканчивается всё семейным обедом — с новыми загадками. Воспитанные молодые люди должны многое уметь и знать, в том числе математику, и их наставники и старшие родственники не упускают случая заставить их попрактиковаться. Здесь же множество книг Рэймонда Смаллиана, в которых логические задачи нанизываются на простой приключенческий сюжет. Русские авторы такого рода текстов, именно художественных, а не просто наборов занимательных фактов и задач, — это Владимир Лёвшин (серия о Рассеянном Магистре) и Сергей Бобров («Волшебный двурог»).
Обыкновенно такие тексты обращены к детям и подросткам, это своего рода романы воспитания. Такая литература молодеет, теперь это скорее задачи для младших школьников, и не потому, что дети стали быстрее решать такие задачи, а потому, что большие дети меньше интересуются такими историями. А жаль!