От эдемского сада до лесных пожаров. Как исследовать мир при помощи клеточных автоматов
Что общего между перемещениями доисторических червей, механизмами дискриминации и распространением эпидемий? Оказывается, все эти процессы описываются при помощи одной и той же математической модели — клеточных автоматов, первым знаменитым примером которой стала придуманная Джоном Конвеем игра «Жизнь». Математик Давид Кац объясняет, как простая игра может вдохновить множество исследований, что за космические корабли бороздят просторы плоской решетки и почему горка песчинок может превратиться в причудливый фрактал.
Основная прикладная ценность современной математики состоит в создании моделей для других областей науки. Мы встречаем какую-то проблему, и прежде, чем приниматься за решение, нам надо описать ее языком математики. Когда проблема описана, мы можем с ней что-то сделать — придумать способ, благодаря которому найдем решение, посчитаем возникающую погрешность либо докажем единственность решения (или обнаружим, что их много), — так или иначе, с задачей мы разберемся. Однако иногда всё происходит ровно наоборот: мы искусственно задаем модель, не отвечающую реальной задаче, и неожиданно оказывается, что она описывает реальные явления — и, более того, становится не только инструментом изучения этих явлений, но и открывает огромный новый мир для исследований. Об одной из таких историй — эта статья.
Клеточные автоматы — дискретная модель, состоящая из регулярной решетки ячеек (не только квадратных, но и, например, шестиугольных), каждая из которых может пребывать в одном из конечного числа состояний.
Для программирования автомата нам следует описать начальное состояние ячеек и правила перехода из одного состояния в другое. Обычно правила перехода задаются в терминах состояний так называемой окрестности, в простейшем случае — состояний соседних клеток. Подобных моделей довольно много, но нужно уточнить, что количество измерений решетки в определении не ограничено — здесь мы в основном будем иметь дело с двухмерными решетками, однако они могут быть и трехмерными, и четырехмерными, и так далее. Есть ограничение на регулярность решетки, но если его снять (например, сделав решетку с ячейками разных форм), мы получим новые модели, которые могут привести нас к чему-то неожиданному и интересному.
Рекомендация
Размышляй медленно, живи полной жизнью. Манифест Неспешной мысли
Приведем простейший пример — возьмем клетчатый лист. Состояния клеток обозначим как 0 и 1. Клетки в состоянии 1 будем закрашивать, а 0 — оставлять пустыми. Пусть начальное состояние автомата — одна клетка закрашена, остальные пусты. Правила зададим самые простые: если у пустой клетки одна из соседних (по стороне или углу) закрашена, то пустая клетка тоже закрашивается. Запустим счетчик ходов и посмотрим, что получится. На первом ходу закрасятся все клетки по соседству от исходной закрашенной. Затем — все их соседи и так далее. Мы увидим довольно простой процесс, который состоит в расширении черного квадрата на нашем листе. Если бы в начальном состоянии закрашенных клеток было больше, мы бы получили больше расширяющихся квадратов.
Интереснее варианты клеточных автоматов, в которых возможна смена состояний в обоих направлениях. Например, если предыдущему автомату добавить правило о том, что закрашенная клетка очищается, когда у нее больше четырех соседей закрашены, автомат сразу начнет работать менее предсказуемо.
В этой статье мы сначала рассмотрим классический пример клеточных автоматов — игру «Жизнь» и ее значимость как модели для изучения реальной жизни и других явлений, а затем перейдем к менее известным автоматам, которые работают в качестве моделей атомизации общества, позволяют изучать механизмы дискриминации, демонстрируют самоорганизацию в очень примитивных системах, показывают процессы возникновения горных пород и многое другое.
Итак, широко известный пример клеточных автоматов — игра «Жизнь».
Она была придумана великим британским математиком Джоном Конвеем в 1970 году по мотивам задачи, поставленной в 1940-м другим великим математиком, Джоном фон Нейманом. Коротко задача формулировалась так: придумать машину, которая в рамках своей деятельности сможет воспроизводить саму себя.
Игра «Жизнь» подразумевает клетчатое поле, где каждая клетка может быть либо «живой» (закрашенной), либо «мертвой» (пустой). Начальную конфигурацию клеток задает игрок, а правила перехода просты: живая клетка с двумя или тремя живыми соседями выживает. При большем числе живых соседей она умирает от перенаселения, при меньшем — от одиночества. В мертвой клетке при наличии ровно трех живых соседей зарождается жизнь. Это классический вариант правил, существуют многочисленные модификации, где берутся другие числа.
Если хотите понаблюдать за поведением фигур или поэкспериментировать самостоятельно, загляните сюда. Обратите внимание: в этой реализации можно как двигаться по одному ходу, так и запустить процесс и наблюдать его. Внизу страницы расположены предзаданные фигуры, подходящие для экспериментов. Самые любопытные эффекты возможны при комбинации различных фигур.
Рекомендации
Интересно, что столь простые правила создают целый мир, который отражает ряд реальных процессов. Начнем с простой фигуры из четырех клеток.

Нетрудно увидеть, что, согласно описанным выше правилам, она со временем не меняется. Такое поведение означает стагнацию: живые клетки застревают в одном состоянии, не развиваясь. Пример посложнее — так называемые медовые соты.

Более общая версия стагнации — осцилляция. Это ситуация, когда фигура через некоторое количество ходов в точности повторяет себя. Вот несколько простых примеров таких фигур.
В автомате возникают и более сложные фигуры — например, так называемые космические корабли. Они способны перемещаться по клетчатому полю, циклически меняя свои состояния. Космические корабли позволяют жизни распространяться по полю и колонизировать его.
Сталкиваясь с уже существующими формами жизни, они сливаются с ними в новые фигуры и иногда порождают сложные формы жизни, а иногда стагнируют или вовсе вместе погибают.
Другой интересный объект — так называемые ружья, сложные фигуры, которые, колеблясь между своими состояниями, порождают космические корабли, как бы стреляют ими. Это позволяет жизни непрерывно двигаться в определенном направлении, сталкиваясь и сливаясь со всем, что она встретит на пути. Результаты этого могут быть различными.
Часто случается, что корабли, достигнув удаленной живой фигуры, вызывают в ней такое бурное развитие, что «колонизированная» жизнь возвращается назад, чтобы поглотить цивилизацию, вызвавшую в ней эти изменения.
Среди различных конфигураций в игре «Жизнь» нельзя не отметить целый класс состояний, которые называются «сад Эдема». Термин становится понятным, если считать переходы между состояниями жизни процессами эволюции. Сад Эдема — такое состояние, к которому не может привести никакое предыдущее состояние, то есть нечто, что создано не эволюцией, а чем-то еще. Сколько точно существует таких садов, неизвестно, но недавно был получен сад Эдема, умещающийся в квадрате 10×10, и доказано, что нет садов Эдема в прямоугольниках меньше 6×6. Если найдете конфигурацию сада Эдема в промежутке между этими значениями — прославитесь.

В игре «Жизнь» к одному состоянию за один ход может приводить не единственное состояние, то есть у конкретной конфигурации могут быть различные «отцы». Открытым остается вопрос о том, существует ли конфигурация, у которой есть отец, но нет дедушки.
У игры «Жизнь» множество модификаций, наиболее известны «Жизнь без смерти», «День и ночь» и «Высокоразвитая жизнь». Здесь мы не будем их рассматривать, однако они обладают особыми свойствами и безусловно заслуживают внимания.
Рассмотрим теперь некоторые другие примеры клеточных автоматов — параллельно с процессами, которые они описывают.
Начнем с автомата, который прекрасно иллюстрирует разнообразие общества и образование в нем гетто. Клетки автомата могут быть пустыми или занятыми двумя видами жителей — треугольниками и квадратами. Те, в свою очередь, могут быть довольны или недовольны собственным положением. Все они слегка шейписты — важно упомянуть, что уровень их предрассудков достаточно низкий (в реальной жизни часто можно услышать оправдания в духе того, что он приемлемо низкий, ничего страшного): они недовольны, только если менее ⅓ их соседей той же формы, что и они. В действительности для индивидуального жителя это низкий уровень, то есть он недоволен, если, например, пять его соседей из шести — другой формы, а четыре соседа из шести другой формы не вызывают у него протеста.
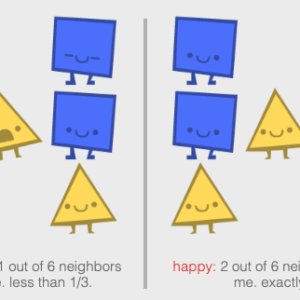
Однако в большом масштабе эти правила оказываются ужасающими: если ваша задача — расселить все недовольные фигуры так, чтобы они стали довольными, то выясняется, что поле достаточно четко делится на области, занятые квадратами, и области, в которых живут треугольники.
Даже если мы произвольным образом расставим квадраты, треугольники и пустые клетки и запустим простой алгоритм, при котором недовольные фигуры по очереди переезжают в первую попавшуюся клетку, где они станут довольными, — окажется, что он очень жестко делит поле на районы по форме. Ниже хорошо видно, как это работает в маленьком масштабе даже при очень разнообразной среде на старте.
А здесь — как это работает в большом масштабе при произвольно заполненной доске.
Интересно, что возможен и обратный эффект: если фигуры требуют, чтобы в их окрестности жило хотя бы 10% фигур другого вида, гетто быстро разваливаются, а фигуры довольно равномерно перемешиваются.
Рекомендации
Эта несложная модель наглядно демонстрирует, как небольшие личные предубеждения создают большую коллективную стену, и добавляет как минимум заслуживающий внимания аргумент в неугасающие споры о западном подходе к вопросам разнообразия, квотировании и о том, какой вклад каждый из нас вносит в общую картину дискриминации и разнообразия.
Кстати, по ссылке есть еще несколько занятных клеточных автоматов, собранных из эмодзи: модель лесных пожаров,
модель хищник — жертва (в данном конкретном случае лисы умудрились изолировать себя от пищи и умереть от голода, а территория оказалась поглощена кроликами — однако модель хорошо демонстрирует баланс экосистем и их хрупкость)
и автомат, посвященный эпидемии неизвестной болезни (sick!), который наглядно показывает феномен коллективного иммунитета — и интересные парадоксы. К примеру, оказывается, что часто вирусы с высокой летальностью убивают меньше людей, чем вирусы с низкой.
Клеточные автоматы — это, как правило, простые модели. Однако оказывается, что даже на таком уровне сложности возникают системы, способные к самоорганизации. Яркий пример — клеточный автомат, называемый «Песчаная куча». Устроен он очень просто. В любой клетке друг на друге лежат песчинки. Если в какой-то клетке лежат четыре и более песчинок, то стопка нестабильна, она разваливается. При этом в четыре соседних по стороне клетки сваливается по одной песчинке. Обвалы будут происходить до тех пор, пока всё поле не станет стабильным — в каждой клетке должно остаться ноль, одна, две или три песчинки.
Настолько простых правил достаточно, чтобы произвольно сложенные стопки песчинок начали заниматься самоорганизацией, выстраивая новые интересные структуры. Даже размещенная в одной клетке высокая стопка песчинок создает причудливые картины, напоминающие фракталы.

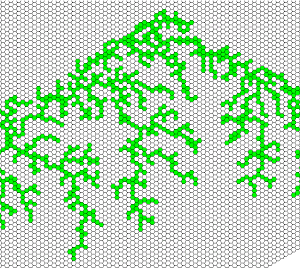
Еще одно семейство клеточных автоматов — черви Патерсона. Это не один, а целый комплекс клеточных автоматов (часто на треугольной решетке), созданных для моделирования перемещений доисторических донных червей. Древние черви должны были перемещаться достаточно близко к уже пройденным путям, чтобы не пропустить небольшие кусочки еды, но при этом не использовать эти пути повторно.

Приведем небольшую галерею из картинок, которые получаются в различных клеточных автоматах. Можно заметить, что некоторые из них похожи на геологические отложения, другие на сети туннелей или на что-то еще. Мы попадаем в интересную ситуацию: мы строим простую модель, а она (иногда внезапно) показывает вполне реальные свойства какого-то явления. Это делает правила такой модели объектом в исследовании самого явления.




Итак, мы увидели, что придумать правила для клеточного автомата нетрудно. При желании легко можно построить несколько ходов на клетчатой бумаге (как, впрочем, и написать код для вашего собственного автомата). Вы вольны экспериментировать — и, вполне возможно, получите что-нибудь новенькое.
